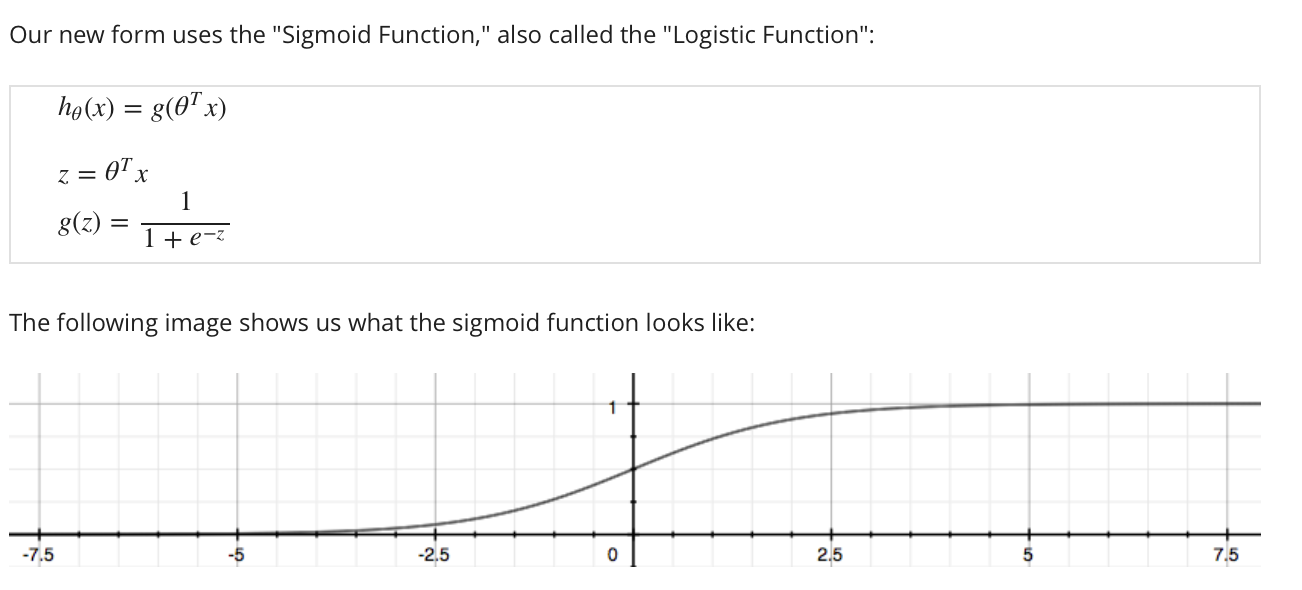
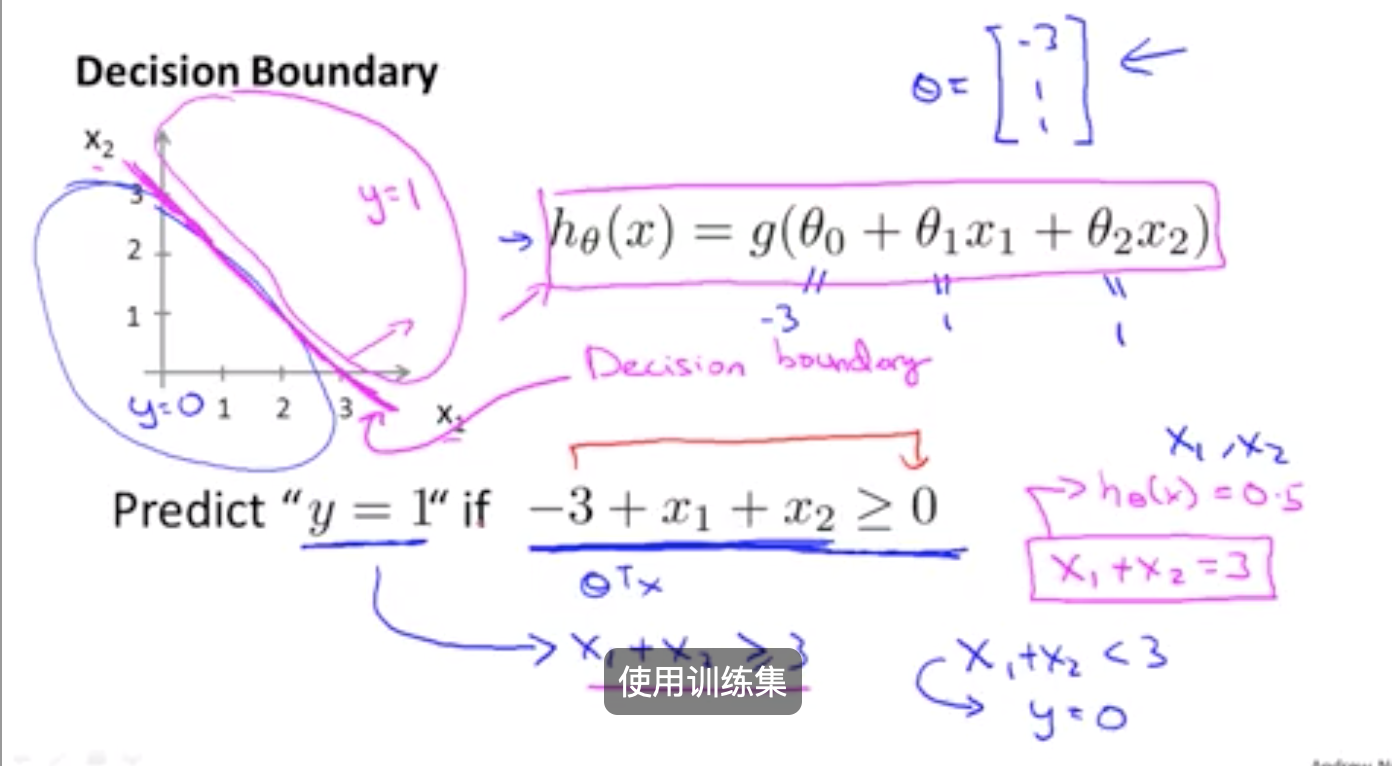
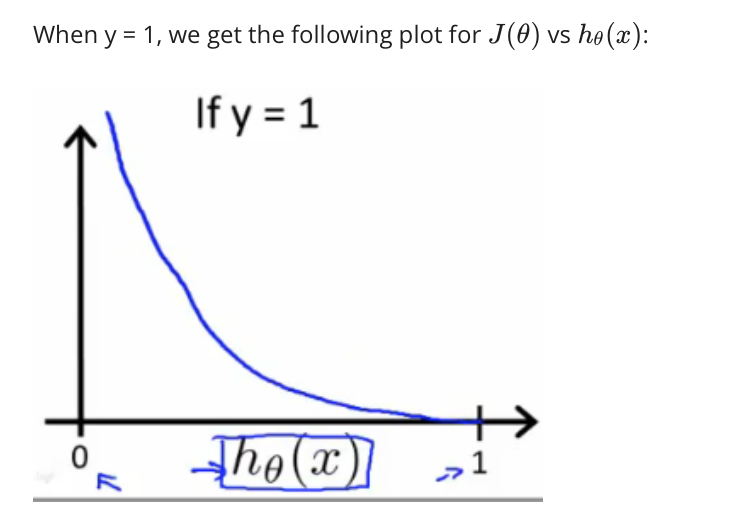
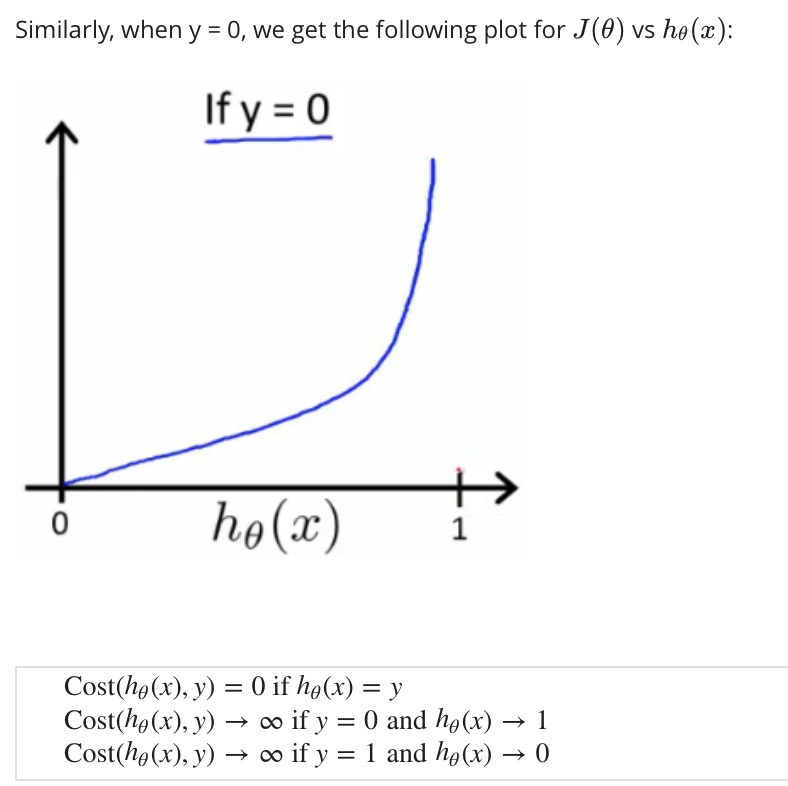
Welcome to MyBlog!

---

信息熵

信息熵的概念

信息熵公式的理解

自信息

引入一个新的概念：自信息：用来衡量某个具体变量或者事件具体发生时，包含的信息量。在这里我们用I(X)表示

如果我们有两个不相关的事件 x 和 y，那么观察两个事件同时发生时获得的信息量应该等于观察到事件各自发生时获得的信息之和，即：I(x,y)=I(x)+I(y)。

因为两个事件是独立不相关的，因此 p(x,y)=p(x)p(y)。根据这两个关系，很容易看出 I(x)一定与 p(x)的对数有关 (因为对数的运算法则是

因此，我们有I(x)=−logp(x)其中负号是用来保证信息量是正数或者零。而 log 函数基的选择是任意的（信息论中基常常选择为2，因此信息的单位为比特bits；而机器学习中基常常选择为自然常数）

I(x)描述的是随机变量的某个事件发生所带来的信息量。图像如图：

信息熵的数学表示

自信息和信息熵的对比：自信息只能处理单个的输出。而熵是对整个概率分布中不确定性总量进行量化

现在假设一个发送者想传送一个随机变量的值给接收者。那么在这个过程中，他们传输的平均信息量可以通过求 I(x)=−logp(x)关于概率分布 p(x)的期望得到，即：

从公式可得，随机变量的取值个数越多，状态数也就越多，信息熵就越大，混乱程度就越大。当随机分布为均匀分布时，熵最大，且 0≤H(X)≤logn

熵和编码长度

信息论中，熵代表着根据信息的概率分布，对信息的编码，所需要的最短平均编码长度。

举个简单的例子来理解一下这件事情：假设有个考试作弊团伙，需要连续不断地向外传递4选1单选题的答案。直接传递ABCD的ascii码的话，每个答案需要8个bit的二进制编码，从传输的角度，这显然有些浪费。信息论最初要解决的，就是数据压缩和传输的问题，所以这个作弊团伙希望能用更少bit的编码来传输答案。很简单，答案只有4种可能性，所以二进制编码需要的长度就是取2为底的对数：

此时已经有些像熵的定义了。回顾一下熵的定义，正是求−log(p)的期望值，所以我们把这个思路也套用一下：

信息的作用

概述

一个事物内部存在着随机性，也就是不确定性，假定为U，而外部消除这个不确定性唯一的办法就是引入信息I，而需要引入的信息量取决于这个不确定性的大小，即I>U才行。当I<U时间，这些信息可以消除一部分不确定，也就是新的不确定性。

反之，如果没有信息，任何公式或者数字的游戏都无法排除不确定性。

案例

直接信息和相关信息，都可以降低随机事件的不确定性。

条件熵

条件熵的概念

为什么“直接的、相关的”信息也能过消除不确定性？怎么判断信息是相关的还是直接的或者是无关信息？ 为此，需要引入一个概念：条件熵、互信息

只要证明 H(X)>=H(X|Y) ，也就说明了多了Y的信息后，关于X的不确定性下降了。

公式的理解

条件熵 H(X|Y) 定义为：Y给定的条件下，X对Y的条件概率的信息熵，对Y的数学期望：

互信息

互信息的引入

这里引入另一个概念：“互信息”是作为两个随机事件“相关性”的量化度量。

当x和y完全相关时，它的取值是1；当二者完全无关时，它的取值是0；

互信息的具体应用

相对熵

概念

相对熵也是用来衡量相关性，但是和随机变量的互信息不同，它是用来衡量两个取值为正数的函数的相关性。

应用

交叉熵

总结

Welcome to MyBlog!

---

1. 通信模型

1.1 简单的通信模型

1.2 通信 与 nlp 的关系

几乎所有的自然语言处理问题都可以等价成通信的解码问题。

1.3 如何解码

在通信中，如何根据接收端的观测信号01,02,03,…来推测信号源发出的信息s1,s2,s3…呢？只需要从所有的源信息中找到最可能产生出观测信号的那一个信息。

用概率论的语言来描述就是：

2.隐性马尔可夫模型

隐含马尔可夫模型并不是19世纪俄罗斯数学家马尔可夫发明的，而是在20世纪，由美国数学家 鲍姆等人发明的。隐含马尔可夫模型的训练方法（鲍姆-韦尔奇算法）也是以他的名字命名的。

要介绍隐含马尔可夫模型，首先还得介绍一下马尔可夫模型。马尔可夫模型的提出，一开始是为了简化统计语言模型的计算。

3. 隐含马尔可夫模型的训练

Welcome to MyBlog!
部分借鉴于博客

---

1. 统计语言模型的提出

1.1 20世纪70年代以前

统计语言模型产生初衷就是为了解决语言识别问题。

一个语音识别系统，听到一下句子：The apple and 「pear」 salad is delicious.
系统它应该如何翻译：The apple and 「pear」 salad is delicious.
还是：The apple and 「pair」 salad is delicious.（pear和pair在英文里发音相同）

科学家们解决以上问题，是通过判断这个文字序列是否合乎语法、含义是否正确。

1.2 20世纪70年代之后

贾里尼克从另外一个角度看待问题，用一个简单的统计模型非常漂亮地搞定了它。

他的想法是：一个句子是否合理，就看看他的可能性大小如何，至于可能性就用概率来衡量。比如上面的“苹果梨和沙拉很好吃”的语音问题，第一个句子出现的概率是10的-20次分，第二个句子出现的概率是10的-25次方。那么，第一个句子是最有可能的。

2. 统计语言模型的数学表示

2.1 贾里尼克提出了一个简单的统计模型

假定S表示某一个有意义的句子，由一串特定顺序排列的词w1,w2,w3….Wn构成的，这里n是句子的长度。那么P(S)就表示S在文本中出现的可能性。

只要把人类自诞生以来说过的话全部统计下，就知道这句话出现的概率了。但是这种方法显然是不可行。因此，需要一个模型来估算P(S)。

但是这里有一个问题，前面的词P(w1),P(w2)都很容易计算，但到了最后一个词Wn，P(Wn|W1,W2,W3,…,Wn-1)的可能性太多，无法估算

2.2 马尔可夫假设

他给出了一个方法，就是假设任意一个词Wt出现的概率只同他前面的词Wt-1有关，于是问题就变得很简单了。

2.2.1 计算过程

2.3 补充：N元模型、高阶模型

2.3.1 n元模型的概念

所谓n元模型，就是假设一个词由前面n-1个词决定。

所以在2.2中提到的马尔可夫假设，就是二元模型。

2.3.2 N一般取值都很小

主要有两个原因：

2.3.3 马尔可夫假设的局限性

在自然语言中，上下文之间的相关性可能跨度非常大，甚至一个段落跨越到另一个段落。三元、四元、甚至是更高阶的模型都不能覆盖所有的语言现象。

3. 模型训练

3.1 “不平滑”现象

3.1.1 原因：零概率和一概率

3.1.2 解决方法1: 卡茨退避法

3.1.3 解决方法2: 删除差值

3.2 语料选取

• 训练语料和模型应用的领域，不能相脱节
• 训练数据通常越多越好
• 在成本不高的情况下，过滤训练数据是需要的

4 扩展

Welcome to MyBlog!

---

1. 中文分词的演变

1.1 查字典

但是它毕竟太过简单，遇到稍微复杂的问题就无能为力了。

1.2 最少词数的分词理论

无法解决二义性问题

1.3 统计语言模型

1.3.1 统计语言模型分词方法 的提出

1.3.2 统计语言模型分词方法 的数学概括

1.3.3 实现技巧

1.3.4 动态规划

1.3.4.1 什么是动态规划

动态规划：就是已知问题规模为n的前提A，求解一个未知解B的一种方法。

1.3.4.2 设计思路

无后效性：某阶段的状态一旦确定，则此后过程的演变不再受此前各种状态及决策的影响

1.3.4.3 算法实例

1.3.4.4 维特比算法

维特比算法是一种特殊的但应用最广的动态规划算法。利用动态规划可以解决任何一个图中的最短路径问题，而维特比算法则是针对一种特殊的图——篱笆网络的有向图的最短路径问题提出的。之所以重要，是因为凡是使用隐马尔可夫模型描述的问题都可以用它来解码。

1.3.5 统计语言模型分词方法的 局限性

2 延伸阅读： 工程上的细节问题

2.1 分词器 准确性的问题

如何衡量分词结果的对与错，好与坏看似容易，其实不是那么简单。说他容易，是因为只要对计算机分词的结果和人工分词的结果进行比较就可以了。说他不容易，是因为不同的人对同一个句子可能有不同的分词方法。比如“清华大学”。

2.2 导致人工分词不一致性的原因

2.2.1 颗粒度的理解

作者不去强调哪一种颗粒度更好，而是指出：在不同的应用中，会有一种颗粒度比另一种更好的情况。
比如在机器翻译中，一般来讲，颗粒度大翻译效果会更好。比如“联想公司”作为一个整体，很容易翻译为：lenovo，如果分词时把他们分开了，就翻译错误了，联想会被翻译为：association。

但是在另一些应用中，比如网页搜索，小的颗粒度比大的颗粒度更好。比如“清华大学”这四个字作为一个词，在对网页分词后，它是一个整体了，当用户查询“清华”时，是找不到清华大学的，这就错误了。

2.2.2 解决方案

2.2.2.1 原理

2.2.2.2 实现方法

• （1）首先需要一个基本词的词表 和 一个复合词的词表
• （2）根据基本词表 和 复合词表，各构建一个语言模型L1 和 L2
• （3）根据基本词表和语言模型L1，对句子进行分词，就可以得到小颗粒度的分词结果了。对应下图的分词器，输入的是字串，输出是词串。
• （4）在第三步的基础上，再用复合词表和语言模型L2 进行第二次分词。就可以得到大颗粒度的分词结果。对于下图的分词器，输入的是基本词串，输出的是复合词串。

  

2.3 总结

Welcome to MyBlog! This article was writed to take note my study of Machine Learning on Cousera.
部分借鉴于博客

---

1 数学符号

2 标准序列模型

2.1 为什么不用标准神经网络

第一点，输入和输出对于不同的例子会有不同的长度 所以,它不是像每一个例子有相同的输入长度 Tx 或有最大的 Yy 值
或许每一个句子都有一个最大长度。 也许你可以填充或用零填充每一个输入 到最大长度，
但是，这似乎始终不是一个好的表示方法

第二点更严重，那就是 像这样的朴素神经网络结构 它并不会共享那些从不同文本位置学到的特征。 尤其是神经网络学到了经常出现的词汇 如果它出现在了位置1， 就会有标识指出这是人名的一部分 因此，这并不好。 如果它自动计算出经常出现 在其他位置 xt 依然能够表明这可能是一个人名 这也许和你在卷积神经网络课程 中看到的过程很相似 你想要的从图像的一部分学到的模式 来快速生成图像的其他部分， 我们希望在序列数据可以实现相似的效果。

2.2 循环神经网络

循环神经网络从左向右扫描数据 每一步，它所用的参数是共享的 所以会有一组参数, 我们将在下一页详细描述。 但是控制从x1到隐藏层的连接 是一组参数，我们用W_ax表示它们 这一组W_ax参数同时 也会被用于每一个步骤 我想我可以在那里写上W_ax 激活函数，各层间水平的链接是由 一组参数W_aa来控制 同样的W_aa也将被用于每一个步骤中 同样，W_ya控制输出预测 我将在下一张幻灯片中详细叙述 这些参数是如何运作的 那么，在循环神经网络中 当预测y3时意味着什么？

这种神经网络结构的一个限制 那就是在一确定的时间内预测 
只使用输入或使用输入序列中之前信息 但不使用序列中后面的信息 我们将在稍后的视频中讨论 
双向递归神经网络或 BRNNs 但现在但现在 这种简单的单向神经网络体系结构 
就足以解释这些关键概念了

2.3 前向传递过程

Waa 和 Wax是共享的，被用于每一个步骤

2.4 反向传递过程

3 不同类型的RNN

(1)输入和输出的数量相同

(2)多对1：假設，您想要來解決情緒分級問題 這裡的 x 是一段文字 可能是電影評論說 “這部電影沒啥看頭” (There is nothing to like in this movie) 所以 x 是一個序列 而 y 或許是一個數字從 1 到 5 或者 0 或 1

(3)1对多：一個一對多神經網路架構的例子是音樂產生器 實際上，您將自己建置一個這種網路 在這個課程程式練習裡，您將會有一個神經網路 輸出一些音符相對於一段音樂 而輸入 x 可能只是一個數字 告訴它您想要什麼類型的音樂， 或者是您想要音樂的第一個音符 如果您不想輸入東西 x 可以是空 (null) 輸入，也可以是零向量 這種神經網路架構裡，您的輸入 x 然後您的 RNN 輸出 第一個值，然後 在沒有任何輸入下做輸出 第二個值，然後繼續下去 第三個值，等等 直到您合成了這段音樂的最後一個音符

(4)编码和解码

4 语言模型和序列生成

4.1 什么是语言模型

案例：

假設我們要建構一個語音辨識系統 當你聽到以下句子: 「蘋果和梨子沙拉很好吃」 
所以你聽到了甚麼 我是說「蘋果和一對沙拉很好吃」還是「蘋果和梨子沙拉很好吃」(注: 
英文中一對(pair)和梨子(pear)同音)

而語音辨識系統挑出第二句的方法 是透過語言模型 來告訴我們這兩句子各自的機率為何 例如, 
一個語言模型可能會說第一句的 機率是3.2乘以10的-13次方 
第二句的機率是5.7乘以10的-10次方 有了這些機率, 第二句是更為可能的 
因為和第一句相比10的指數多3 所以系統會挑出第二句

語言模型做的事是給定特定句子 它能告訴你特定句子的機率為何 我說的機率是指, 如果你想拿起隨機一份報紙, 隨機打開一個電子郵件或一個網頁或 聽你的朋友說的下一件事 此特定句子, 比如說剛提到的蘋果和梨子沙拉 在這世界中被使用到機率為何 這是以下兩者的基礎要件: 剛提到的語音辨識系統 和機器翻譯系統 我們會期望它輸出最有可能出現的句子

因此, 語言模型的基礎工作是輸入一個 我會將其寫成y^<1>, y^<2> 到 y^的句子 語言模型做的是將句子表示為 y 而不是 x, 但語言模型做的事是預測 該特定字詞序列的機率

5 如何构建语言模型

• 首先我们需要一个大型的语料库（Corpus)
• 将每个单词字符化
• 2个特殊的单词：EOS（ end of sentence 终止符）、UNknown（字典里没有收录的字词）

之所以将真实值作为输入值很好理解,如果我们一直传错误的值，将永远也无法得到字与字之间的关系。

6 新序列的采样

7 如何解决梯度消失的问题

7.1 梯度爆炸

你還記得我們也提到非常深層的神經網路 也有提到梯度爆炸的問題 當進行反向傳播時 梯度不僅可能呈現指數下降 當計算到越深層時, 也可能呈現指數上升 事實上, 當訓練RNN網路時, 儘管梯度消失是較為嚴重的問題 但梯度爆炸也是有可能發生 這可能使神經網路崩潰 因為指數項非常大的梯度可能會造成 參數也隨之變的非常大, 讓神經網路無法被使用 而梯度爆炸很容易被發現 因為你的參數可能會變成 NaN 或者是 顯示為非數字的情況 代表神經網路計算中出現數值溢位問題 如果你真的遇到了梯度爆炸 有可解決方法是運用梯度修剪(gradient clipping) 它代表的是 觀察你的梯度向量 如果它大於某個閾值 重新縮放梯度向量, 確保它不會太大

7.2 梯度消失

這是一個非常深的網路 假設有100層或更多, 你會從左至右做正向傳播 然後再做反向傳播 我們曾說過, 如果這是很深的網路 那從輸出 y 得到的梯度 會非常難以做反向傳播 並進而難以影響前面幾層的權重 難以影響這裡的計算

8. GRU(gated recurrent unit 门控循环单元)

8.1 门控单元的原理

(Gate Recurrent Unit) 一種修改 RNN 隱藏層的方式，使得它更能捕捉 長距離的連結， 對於梯度消失問題有很大幫助

对RNN的一个隐藏层可视化：

您或許需要記住，貓 (cat) 是單數 來確定您理解為什麼使用 “was” 而不使用 “were” 所以 “cat was full” 或者 “cats were full” 當我們從左到右讀這一段句子 GRU 單元將會有一個新的變數稱為 c 代表細胞 (cell) 記憶細胞 而記憶細胞的作用是提供一點點記憶來記住，舉例 貓 (cat) 是單數還是複數 所以當它進入這個句子更後面時 它還可以在工作時考慮到 句子的主題 是否是單數還是複數 所以在時間 t 時，記憶細胞會有一些值 c

gammaU、C、C候选值，可以是向量，gammaU不一定全是0/1，只是逐元素告訴 GRU 單元 哪一些位置，只是告訴您哪些 記憶細胞的維度需要在每個時間步驟中更新 所以您可以選擇保持一些位置不變 當更新其他位置時 舉個例子，或許您可以選擇一個位置來記住 貓是單數還是複數，或許使用 其他一些位置來記住您談的是有關於食物

8.2 门控单元的优点

因為 gamma 可以相當接近 0 可能是 0.000001 甚至更小 它不太會有梯度消失的問題 因為您說 gamma 相當接近 0 這個基本上會讓 c 等於 c 而 c 的值會相當程度的保留 即使經過了很多很多時間步驟 所以這個可以明顯地幫助解決梯度消失問題 而讓神經網路可以使用甚至更長的距離的依賴性

8.3 完整版GRU

9. LSTM 长短期记忆单元

LSTM 的一個新特性是 並非只用一個更新門閘來控制記憶過程 如這裡的兩個項 我們是用兩個不同來源的項 我們不再只用 Γᵤ 和 (1-Γᵤ) 而是在這裡用 Γᵤ 然後用遺忘門閘 Γf 那這個 Γf 門閘 用到了 sigmoid S型函數
其它和你之前看到的差不多 這裡是 x 並加上 bf 然後我們會有一個新的輸出門閘 一樣是sigmoid S型函數, 用到 Wₒ 最後加上 bₒ 然後, 記憶細胞的更新值 c 等於 Γᵤ 這個 ＊ 表示矩陣中逐元素的乘積 這是個向量間逐元素乘積 再加上, 取代 (1-Γᵤ) 用的是另一項遺忘門閘 Γf 乘以 c 這樣給了記憶細胞選擇權 去決定使用多少舊數值 c 並直接加上新的值 c~ 所以這裡是使用兩個分開的項, 更新門閘和遺忘門閘 這些代表更新門閘, 遺忘門閘, 還有輸出門閘 最後, 取代 GRU 中的 a=c a 等於輸出門閘和 c 去做逐元素乘積 那這就是 LSTM 的主要方程式 它用了三個門閘, 而並非兩個 並把三個門閘用到了不同的地方

10. 双向RNN模型

「雙向 RNN 模型」 它讓你在序列的某個時間點上 可以同時獲得過去或未來的資訊

這就是雙向 RNN 的運作 而這些 RNN 單元不僅可是標準的 RNN 單元 也可以是 GRU 或是 LSTM 單元 事實上, 大多是自然語言處理問題 特別是有大量文本的問題 有 LSTM 單元的雙向 RNN 是很常被使用的 所以, 如果你遇到了 NLP 問題, 而且句子都是完整的 並想嘗試標記這些句子 一個有 LSTM 單元的雙向 RNN 有前向和反向的計算, 應該會是你的首選

11. 深度RNN

在上图所示框架基础上

，可以改进的地方（1）： 在RNN之后，然後用一些深度層但不用水平連結 使用深度網路來最後預估 y<1> 您可以用相同的深度網路來預估 y<2> 所以這種網路架構比較常見 您有三個遞迴單元以時間相連 連結一個網路 之後連結一個網路 就像 y<3> 跟 y<4> 一樣 這裡有深度網路，但這些並沒有水平連結 所以這是一種比較常見的架構

改进（2）：這些區塊不只一定是標準的 RNN 簡單的 RNN 模型 它們也可以是 GRU 區塊，或是 LSTM 區塊

改进（3）：您也可以在雙向 RNN 上建立深度版本

Welcome to MyBlog! This article was writed to take note my study of Machine Learning on Cousera.

---

1. 迁移学习

1.1 什么是迁移学习

是有时你可以把在一个任务中神经网络 学习到的东西，应用到另一个任务中去。 比如，你可以让神经网络 学习去识别物体，比如猫，然后用学习到的 （一部分）知识 来帮助你更好地识别X射线的结果。 这就是所谓的迁移学习。

例如放射扫描结果的诊断过程 即真实地读取X光扫描图像 你可以做的就是，取出这个神经网络的最后一层 并移除掉这一层以及其相关的权重 然后为最后一层神经网络创建一个新的随机初始化的权重 使用新建的这个输出层来进行放射结果的诊断 所以，具体来说，在训练模型的第一阶段， 当你在做图像识别的任务时， 你训练了所有常用的神经网络的参数，所有权值 所有层，然后这个模型 现在能够做出图像识别的预测。 训练得出了这样一个神经网络之后， 要实现迁移学习，你现在需要把数据集X和Y 设定为放射影像。 现在的Y是你想要预测的诊断结果， 你要做的是初始化最后一层的权值 我们叫这个为WL 和PL。 然后现在，重新在新的数据集上训练这个神经网络， 就是新的放射数据集上。

你有几种方法来重新训练这个放射数据的神经网络。 如果你只有一个小的放射数据集， 你可以只重新训练最后一层的权值，就是WL 和PL，同时保留其它所有参数。 如果你有足够的数据， 你也可以重新训练神经网络的其余所有层。 我们的经验就是如果你有一个小规模的数据集， 那么就去重新训练最后一层和输出层的神经网络， 或者你也可以训练最后一到两层的神经网络。 但是如果你有大量的数据， 你或许可以对这个神经网络的所有参数都进行重新训练。 要是你对神经网络的所有参数进行重新训练， 那么这样训练的初始化阶段 有时候被我们叫做预训练（pre-training） 原因是，你在是使用图像识别的数据 来预初始化（pre-initialize）或者说预训练神经网络的权重。 然后如果你在之后对所有的权重进行更新， 那么在放射扫描的数据上的训练有时候被我们叫做微调（fine tuning) 所以有时候你会在深度学习领域听到预训练（pre-training）和微调（fine tuning）这些词， 上面我所说的就是他们在迁移学习中 表达的真正含义。

一个迁移学习不适用的例子是， （上面讲到的）数据规模被颠倒过来的时候。

1.2 迁移学习什么时候适用

• 如果你尝试 从某个任务A中学习到的信息迁移到某个任务B中， 那么当任务A和任务B在有相同的输入时，迁移学习才能适用。

• 必须在任务A比任务B有更多的数据时，迁移学习才适用。 所有条件都是在想要把任务B做好的前提下 因为在任务B中的数据比在任务A中更加地有价值， 通常你需要为任务A准备更多的数据，因为 在任务A中的样本比任务B中的样本价值更低。

• 迁移学习更加适用的场景 是当你认为，任务A中的低层次特征会帮助任务B达成目标。

2. 多任务学习

2.1 什么是多任务学习

在多任务学习中,你（多个任务）一起开始 尝试让一个神经网络同时做几件事 
然后,每个任务将会帮助完成其他任务。 我们来看个例子让我们来看一个例子

你可以有一个神经网络以x作为输入和 输出为四维的y。 请注意这里的输出,我已经绘制了四节点。 第一个节点,我们试图检测是否有行人 在这张图片中 第二个输出会检测到是否有辆车 还会检测到是否有个停车标志和红绿灯

所以这里的y^是四维的。为了训练这个神经网络,你需要定义 这个神经网络的损失函数 预测输出的y^(i)是4x1维的。 损失是整个训练集的平均损失 为1除以m，乘以从i=1到m的总和 j从1到4各自预测的损失

它只是将4个部分行人、车、停车标志 红绿灯进行相加 这里的L是普通的逻辑斯蒂损失函数。

把这写下来 所以就是 yj(i)logŷj(i)+(1-yj(i))log(1-ŷj(i))

和softmax回归区别是,不像softmax 回归,它将单个标签分配给单个示例。 这一个图像可以有多个标签。

2.2 什么时候适用多任务学习

1 你要训练一系列的任务可以 共享一些低层次的特征 自动驾驶的例子中,在识别交通灯 汽车和行人时,都有相似的特征 这可以帮你识别停车标志，因为他们都是道路特征

2 其次——这不是硬性的规则,所以不总是存在的—— 但我看到很多成功的多任务学习，他们 每个单项任务的数据量非常相似。

如果神经网络不够大，多任务学习 与单项训练相比会损害准确率。 但如果你训练足够大的神经网络,那多任务学习 应该不会或很少影响性能。 与你分别单独训练不同任务相比， 它实际上能够提高性能。 这就是多任务学习。 实际上多任务学习要比迁移学习用得少得多。

3. “端到端”的机器学习

什么是“端到端“的深度学习呢？ 简单地说，我们有一些数据处理系统 或者是由多个阶段组成的学习系统 端到端的深度学习做的 就是它可以捕获所有的阶段 并且，通常可以将其替代为单个神经网络 也就是说运行速度更快

所以，如果端到端深度学习可行， 可以非常有效和简化系统，且 不用建立很多手工设计的单个组件。 但是它不是万能的， 它并不总是有效。

3.2 端到端的优缺点

优点1: 端到端学习真正地让数据发挥主导作用 所以如果你有足够的(X, Y)的数据 那么不论那个能最好地将X映射到Y的函数是什么样子 只要你有足够大的神经网络 顺利的话，神经网络都能拟合出来 通过单纯的使用机器学习方法 你的神经网络能够更好从输入的X->Y中 学习到数据内在的统计学特性 而不是被迫去反映人的先见

优点2：所需的人类动手设计的组件变的更少了 所以这可以简化你的设计工作流程 意味着你不需要话大量的时间去动手设计特征 手工设计这些中间表示形式

缺点1：第一，端到端学习需要大量的数据 所以为了使用机器学习直接得出X到Y的映射 你或许需要大量的(X，Y)数据

缺点2: 它排除了一些具有潜在用途的手工设计组件 所以机器学习研究人员往往会轻视手工设计的组件 但是如果你没有足够的数据 那么你的学习算法就不能够洞悉你数据中的规律 如果你的训练集很小 所以手工设计的组件的确是一条可行之路 去将人工知识融入到算法中 而且这并不总是个坏主意 我认为学习算法有两个主要的知识来源 一个是数据，另一个是你手工设计的东西 这些东西可以是算法中的组件，或者是特征，或者是其他的东西 所以如果你有很多很多的数据 手工设计就没那么重要了，但是如果你没有那么多的数据 那么有一个精心手工设计的系统实际上可以让人们向 算法中注入人类关于这个问题的知识

Welcome to MyBlog! This article was writed to take note my study of Machine Learning on Cousera.

---

1. 错误分析

什么叫表现上限：

拿大约100张分类错误的验证集图片<br />并进行手动检测 只需要数一数 看有多少张 
验证集中标错的样本实际上是狗的图片 现在 假设事实证明 在验证集中分错的100张样本里<br />
有5%是狗的图片 也就是说 验证集中<br />分错的100张中有5张是狗 这意味着在这100张图片中 
特指你分错的这100张 即使完全解决狗的问题<br />也只在这100张中多分对了5张 换言之 
若只有5%的错误是狗照片 如果你在狗的问题上花了大量时间 最好的情况也就是 你的错误率 
从10%下降到9.5% 对吗 这5%是错误里的相对下降值<br />因此是从10%下降到9.5% 
那么你可能可以合理地判断出

错误分析：

假设有别的事情发生了 假设 在验证集里错标的100张样本中 你发现他们中的50张实际上是狗的图像 所以50%是狗的照片 现在你可以更确定地把时间花在狗的问题上 在这种情况下 如果你真的解决了狗的问题 你的错误率可能将从这10%下降到5% 你可能会认为错误率减半是值得付出努力的 专注于减少被错误标识的狗 我知道在机器学习中 有时我们会贬低 手动操作或使用太多人工判断 但是如果你在构建应用系统
那么这个简单的计数过程 也就是错误分析 可以节省你很多时间 在决定什么是最重要的 或哪个方向最有希望 值得关注

2. 如何对待错误数据

1 当错误数据发生在 训练集

事实证明，深度学习算法 对训练集中的随机错误很稳健 只要你的错误，或者说错误标记的例子 只要这些错误不是那么偏离随机分布 而可能只是由标记的人偶然的疏忽造成的， 比如随机按下了错误的键 总之，如果这些错误是相当随机的 那么我们基本可以不管（这些错误） 不用花费太多的时间去纠正它们 当然了，仔细检查你的训练集和标签 并且纠正它们，肯定是无害的 有时候，这是很值得花费时间去做的， 但你也可以不做，只要总数据量够大， 而且实际错误标记的数据占比不高

2 这些错误标记的数据（对开发集和测试集）的影

一个比较推荐的做法是，在错误分析的过程中 增加一列，去统计 Y的标签错误的数量

如果这些错误对你评估算法在开发集上的效果 有很大的影响的话 那就继续做吧，花时间去纠正这些错误标签 但是如果没有太大影响 对你用开发集去评估模型 那你的时间最好不要花在这上面

3 如果你决定探究开发集 手动重新检查标签，并且尝试纠正一些标签 这里由一些额外的指南或者说原则去考虑

(1) 如果你要探究并纠正开发集中的一些问题 我会建议将这个过程也应用到测试集，以确保 它们依然服从同样的分布

（2）我强烈建议你考虑检查 你的算法准确预测和错误预测的例子（这个原则不常被使用，因为判断正确的数据太多）

(3) 训练集 和 开发/测试集，可能来自不同的分布

3. 如何快速构建一个新的系统

我的建议是
快速构建你的第一个系统 然后迭代 这个建议不那么适用
如果你处于一个 你经验丰富的领域 这个建议同样也不适用于 当有很多可以参考的学术论文 针对你正在研究的
几乎完全相同的问题 比如说 有很多学术文献研究人脸识别 如果你正在尝试建立人脸识别系统 你可以从一开始就打造一个复杂的系统 依托于大量的学术文献 但是 如果第一次
你正在研究一个新的问题 那么我建议你 真的不要考虑太多
也不要把你的第一个系统做得太复杂 只要建立一个快速的早期的系统
然后使用它 来帮助你确定一个优先级
如何来改善你的系统

4. 当training 和 test数据来自不同分布

方案一，将两个集合的数据混合在一起，再重新分配(建议不要采用方案一 因为它设置的开发集使你的团队致力于 优化一个与你实际关心的目标
并不相同的数据分布)

这样的数据分配有其优点和缺点 优点是这样一来你的训练/开发/测试集 都来自于同一分布 易于管理 而缺点 一个巨大的缺点是 仔细看看你的开发集
它有2,500个样例 但是大部分来自网页图片的分布 而不是你真正关心的
来自移动应用图片的分布

方案二：假设训练集仍然包含205,000个图片，练集包含200,000个网络图片 和5,000个移动应用图片 开发集包含2,500个移动应用图片 测试集也包含2,500个移动应用图片 按照这种方式划分训练/开发/测试集 其优点是你瞄准的是正确的目标 你在向你的团队表明
我的开发集数据来自于移动应用 而这正是你真正关心的图片的分布 让我们来建立一个机器学习系统 它在移动应用图片分布的表现的确很好 当然其缺点就是你的训练集的分布 不同于您的开发和测试集分布 但事实证明这样划分训练/开发/测试集 长期来说性能更好

5. 不匹配数据分布的偏差和方差

通过估计学习算法的偏差和方差 能帮你确定下一步工作的优先级 但当你的训练集 开发集 测试集 来自不同的分布时 偏差和方差的分析方法也会相应变化

这时误差分析要注意 当你从训练集误差 转移到开发集误差时 有两件事情变了 一 算法看到的数据只有训练集没有开发集 二 开发集和训练集数据分布不同 因为同时存在两个变量 我们很难判断 这9%的误差 有多少是因为 算法未接触开发集 而影响了方差 又有多少是 因为开发集的数据分布不同

为了辨识出这两个影响 如果你对这两种影响完全不了解 别担心 别担心 我们马上就会说到 为了梳理出这两个影响 我们需要新定义一组数据 叫做训练-开发集(training-dev set) 这是一个新的数据子集 我们要让它与训练集拥有同样的数据分布 但你不用直接拿它来训练你的网络 就是这样子

之前我们已经建立了训练集 训练集和测试集 如图所示 开发集和测试集属于同分布 训练集数据属于不同分布 我们要做的是将训练集随机混淆(shuffle) 取出一小块数据作为训练-开发集 如同开发集与测试集分布相同 训练集与训练-开发集也遵循相同分布

假设训练集误差为1% 训练-开发集误差为1.5% 但是开发集误差为10% 这就是方差偏小的问题 因为从已经见过的训练集数据 到未见过的训练-开发集 误差只增加了一点点 但是到开发集出现了跃增 所以这是数据不匹配的问题

6. 如何解决因为数据不匹配导致的误差

如果发现出现了严重的数据不匹配问题 我通常会人工地分析误差 并且试着去理解训练集与开发/测试集之间的差异 为了避免测试集上的过拟合 技术上对误差分析来说 你的关注点应该只是开发集而不是测试集

如果你的目标是使训练集与开发集更加相似 这样有什么解决方法呢？ 其中一个方法是你可以通过 人工数据合成 让我们在解决汽车噪声问题的背景下讨论这个问题。

Welcome to MyBlog! This article was writed to take note my study of Machine Learning on Cousera.

---

1 机器学习策略

1.1 什么是机器学习策略？

有快捷高效的方法 分辨出在之前提到的或者没有提到的各种想法中 哪些值得进行尝试 哪些可以直接放弃
一些基本套路 也就是一些分析机器学习问题的方法 这些方法 会让你避免南辕北辙

1.2 正交化过程（调参，参数之间互不干扰）

建立机器学习系统的挑战之一是*有太多可以尝试和改变的东西**，例如调整的超参数。
最高效的机器学习人员都非常清楚需要调整什么，我们称这一过程为正交化***。

实例：

正交化就是指电视设计师 So in this context, orthogonalization refers to that 
the TV designers 在进行设计的时候 确保每个旋钮只能进行一个参数的调整 had designed 
the knobs so that each knob kind of does only one thing 
而这让电视屏幕的调整变得更加容易 And this makes it much easier to tune the TV, 
so 使得电视画面能够显示在你希望的位置上 that the picture gets centered where you 
want it to be.

为保证有监督脊椎的学习系统良好地运行，调整系统旋钮，保证四件事准确无误。

（1）通常确保至少训练组运行良好。因此训练组的运行情况需要进行一些可行性评估。
如果训练组表现良好, 你将希望这能使开发组运行良好，同时 你也会希望测试组运行良好， 最终 你希望能在成本函数的测试组里运行良好，因为结果会影响系统在实际情况中的表现， 因此 希望这能顺利地实现,

（2）相反，如果你发现算法对dev集的拟合结果不太好 那么 就需要另一套独立的旋钮 是的，这就是我画的不太好的，另一套旋钮 你需要有一套不同的旋钮 来调整(开发集的拟合结果)

（3）如果（算法）在dev集上表现很好 但是在测试集上不行呢？ 如果这样， 你可能想要一个调整的旋钮 用来获取一个更大的dev集 因为如果（算法）在dev集上表现很好 但测试集上不行，这可能意味着， 你过度调节了dev集 你需要返回去，寻找一个更大的dev集

（4）如果（算法）在测试集上表现也很好 但是依然不能给你 愉快的用户体验，这意味着你需要返回去 调整你的dev集或者成本函数

2. 单数评价指标

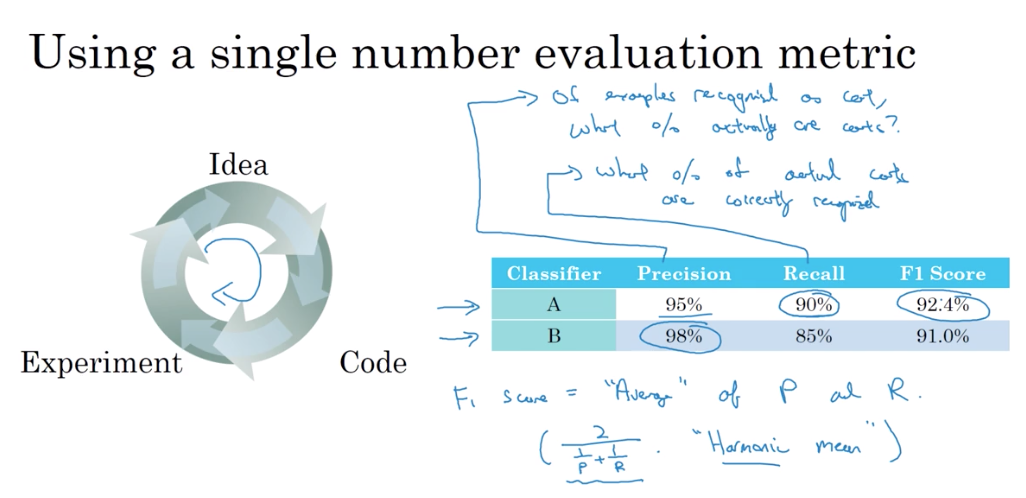
2.1 F1 score

因此分类器A有95%的精准率 就意味着 A如果把一张图片分类为猫 那么95%可能它就是猫 
而召回率就是 对于所有是猫的图片 你的分类器有多少百分比可以正确的识别出来 
即多少比率的真猫被正确的识别出了

2.2 满足指标（satisficing matrics）和 优化指标（optimizing matrics）

如果你同时关心多项指标， 你可以将其中的一样设为优化指标， 使其表现尽可能的好 ，将另外的一项或多项设为满足指标，确保其表现满足要求，大多数情况下他们都会优于最低标准，这样一来你就有了一个几乎自动的， 快速评价模型和选择”最佳”模型的方法

例子：
你决定关注 猫分类器的分类准确率(accuracy) 它可以是F1分数(F1 score)
或者别的什么精确度度量 但是假设 除了准确率之外你还关心运行时间
也就是对一个图像分类需要多少时间
这个表中分类器A需要80毫秒(millisecond)
B需要95毫秒 C需要1,500毫秒 也就是1.5秒才能甄别一个图像
你当然可以将准确率和运行时间组合成一个 整体评价指标(overall evaluation metric)
比如说整体代价是 准确率-0.5*运行时间 但是将准确率和运行时间用这样的公式整合
看起来有些刻意 这就像二者的线性加权和(linear weighted sum) 所以你还可以这样做:
你可能想要选择一个分类器 它在确保运行时间的前提下提供最大准确率
比如说它甄别图像所花费的时间 必须<=100毫秒 在这个例子中我们说准确率是优化指标
因为你想要最大化准确率 你希望准确率尽可能的高 但是运行时间是我们我们所说的满足指标
意味着它必须足够好 必须<100毫秒 一旦超出即不予考虑 至少不大考虑
所以用这种方式对准确率和运行时间

3. train/dev/test

3.1 开发集（dev）和测试集 应具有相同的分布

dev set 也被称为development set 或者有些时候被称为交叉验证集

机器学习的工作流程是 你尝试了很多想法, 在训练集上训练不同的模型, 然后使用开发集来 评估不同的想法,并选择一个。 并且，保持创新， 提高模型在开发集上的表现性能 直到最后你有一个很高兴的结果 然后你在测试集上评估它们

设置开发集 和检验方法 直接决定了你的目标 将开发和测试集取在同一分布上 你才真正瞄准了你和你团队的目标 你选择训练集的方法 会影响你击中目标的精度

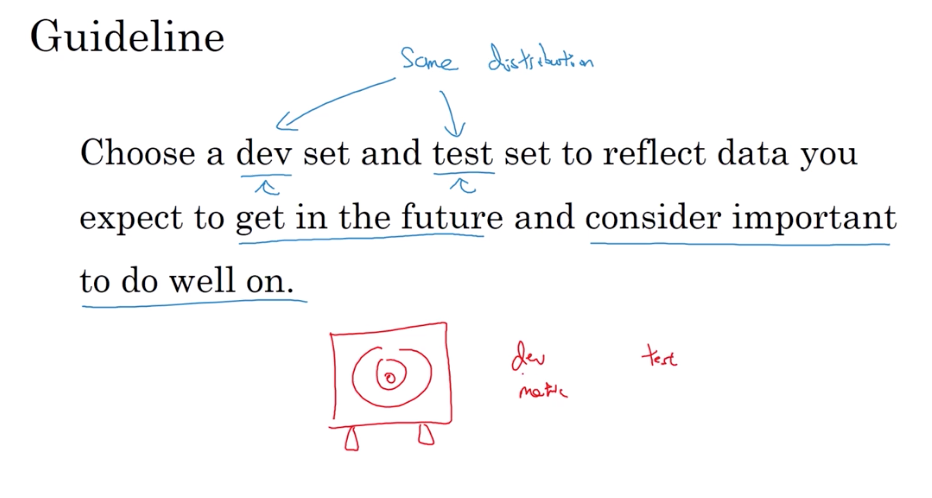
3.2 训练集、开发集、测试集的数据分布

该内容在之前的博客上已经记录过，在此不再赘述，blog

3.3 改变 开发集/测试集 和 评估标准

我们已经学习了如何设置开发集和评估指标 这就好比确定你的团队要瞄准的靶子 可有时候 项目进行到一半 你可能会发现 靶子放错了位置 这时候 就应该移动你的靶子

当你发现评估指标 无法对算法的优劣给出正确的排序时 那么就需要考虑定义一个新的评估指标 这里的例子只是定义评估指标的一种方法 评价指标的目的是为了能够准确地告诉你 给出两个分类器 哪一个更适合你的应用 就本次视频的目标而言 大家不需要太关心如何定义新的误差指标 重点是 如果你对原有的误差指标不满意 那就不要将就着使用这个你不满意的指标 而是定义一个新的指标 使其能够更好地 反应你的偏好 以符合你对更好的算法的定义

3.4 定义评估指标十分重要

4. 和人类级别绩效 比较

4.1 为什么和人类级别绩效比较

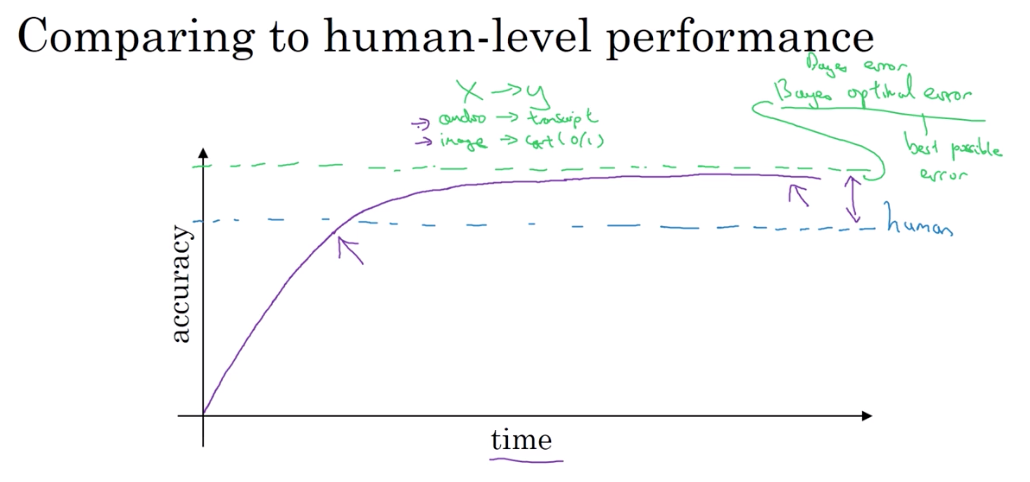
当你继续训练算法时 也许是越来越大模型和更多更大的数据 其效果逼近但从来不会超越一个理论值 这称为贝叶斯最优误差 所以贝叶斯最优误差就是最小的理论误差值

举例：

这就是用 从x到y的任何函数映射超过一定的准确度 
例如对于语音识别，如果x是音频，一些音频就是 太多吵噪而无法判断它在讲什么 
所以理论准确度可能不是 100% 或是猫识别 一些图像很模糊，它是不可能让 
任何人或其他什么事物认出那幅画里有一只猫 所以，精度的完美水平可能不是100％ 
贝叶斯最优误差，贝叶斯最佳误差或贝叶斯错误 简而言之，是从x到y映射的最好的理论函数

事实证明，进度往往相当快 直到你超越人类的表现

你若超越了人类的表现，有时反而慢下来 我认为有两个主要原因 为什么当你超越人类级别的表现时进展往往放慢 原因之一，人类级别的表现 在许多任务中都离贝叶斯最优误差不远 人非常擅长看着图像去分辨是否有一只猫 或收听音频并写出字幕。 因此，可能算法超越人类级别的表现之后并没有，那么大的改善空间

第二个原因，只要你的表现还不如人类水平 那么实际上你可以用某些工具来提高 而当你超越了人类的水平后，就很难再有工具来提高了 就是这样子

只要你的机器学习算法 比人类更糟糕，你就可以从人类得到数据标记 这是你可以问人，问聪明的人，为你的例子标签 这样你可以有更多的数据以满足你的学习算法 我们下周会讲的是手动误差分析 只要人类仍表现优于任何算法，你可以 让人看看你的算法算错的例子，然后了解 为什么人可以做到，但该算法却搞错了。你也可以得到更好的偏见分析和 方差，一旦你的算法做的比人类优异 这三招将变的很难应用

4.2 可避免误差（avoidable bias）

贝叶斯误差和训练集上的误差 之间的 距离，称为可避免的偏差。

模型在训练集与开发集上的误差之差 则是对模型中存在的方差问题的度量

4.3 理解人类级别表现（human-level performance）

把人类误差当做贝叶斯误差的替代值或估计值
有一个好的贝叶斯误差估计 可以很好的帮助你评估可避免的偏差和方差 
从而更利于做决定究竟是专注于偏差降低技术 还是方差降低技术
这个方法在你超越人类水平表现之前是一直有效果的

不管你使用普通医生的还是 一个专业医生的或者是一个有经验的医生团队的 因为这里是4%或4.5% 这明显要大于方差误差（1%） 你必须要确保终止循环的条件一定会达成 你需要专注与降低偏差的技术比如训练更大网络 在让我们看第二个例子 比如你的训练误差是1%而你的验证误差是5% 出学术目的外 无论你选择1% 0.7%或是0.5%哪个 作为人类水平的表现都没有什么区别 因为不管你用哪个定义 你可避免误差的度量 我猜差不多是0%到0.5% 对不对？ 这是人类水平的表现和你训练误差的差距 而这里的差距是4% 因此4%在这里要远大于可以避免的偏差 所以你需要专注于方差降低的技术 比如正则化或者使用一个更大的训练集 但是真正有问题的时候是如果你的训练集误差为0.7% 当然这已经非常好了 而你的开发集误差为0.8% 在这种情况下把你的贝叶斯误差估计定为0.5%就很有必要了

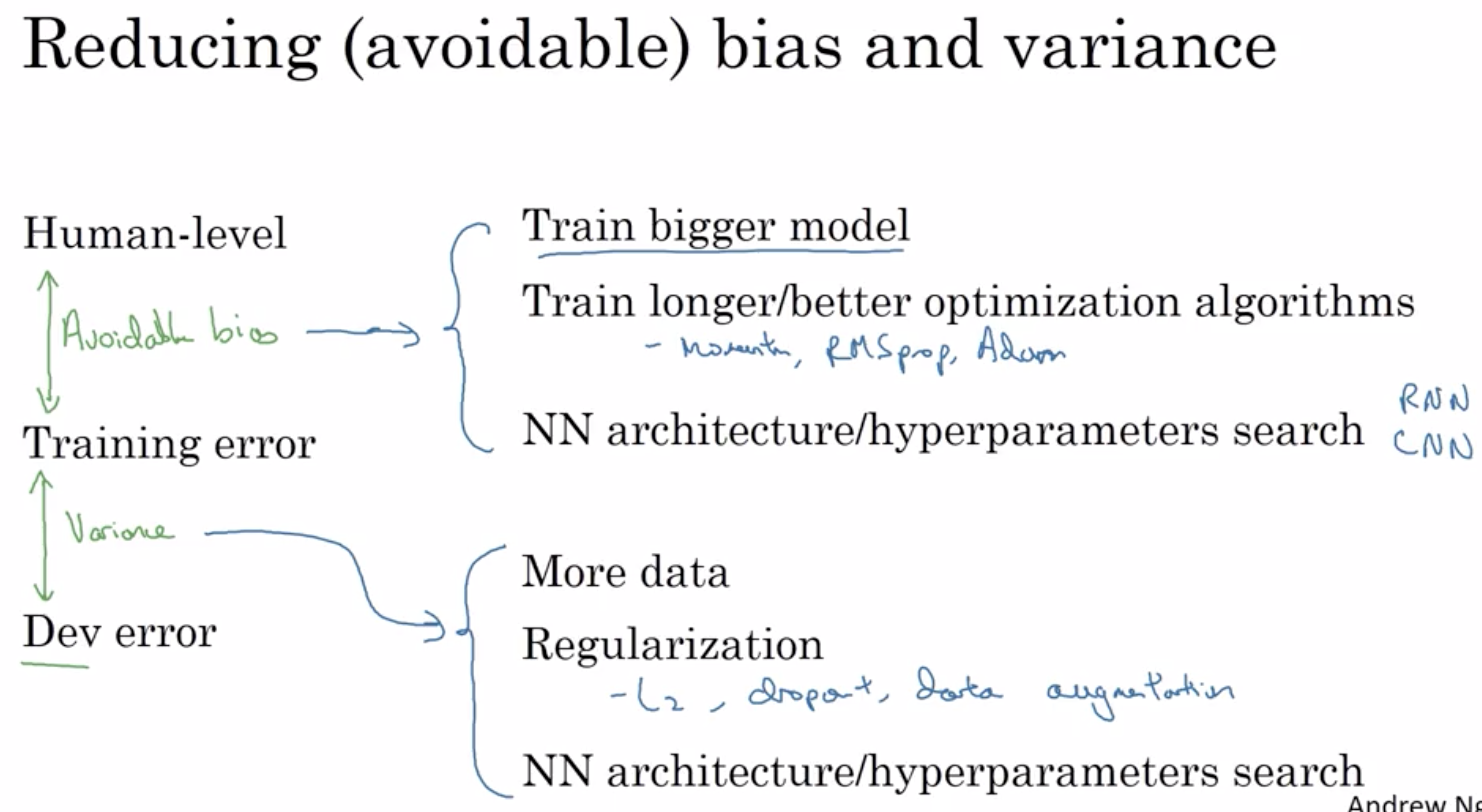
4.4 总结：如何提高你的模型表现

一般，认为一个有监督学习算法能发挥作用，基本上意味着，希望或者预设你可以做到两件事 第一是你可以很好地拟合训练集，你可以大致认为你能得到较低的可避免偏差。

第二点是 训练集的结果可以很好地，推广到开发集或者测试集 这就是说 方差不太大 从正交化角度来说 你看到的是 存在一组旋钮
可以修正可避免偏差的问题 比如训练更大的神经网络
或者训练更长时间 并且有另一组独立的方法
可以用来处理方差的问题 比如正则化或者获取更多训练数据

Welcome to MyBlog! This article was writed to take note my study of Machine Learning on Cousera.

---

1. 用线性回归训练二分类器

原文：分类问题其实和回归问题类似

To attempt classification, one method is to use linear regression and map
all predictions greater than 0.5 as a 1 and all less than 0.5 as a 0.
However, this method doesn't work well because classification is not 
actually a linear function

The classification problem is just like the regression problem.

2. 逻辑回归 （sigmoid函数、逻辑函数、S函数 基本是同义词）

2.1 函数表示(假设函数)

2.2 决策边界（decision boundary)

决策边界是 假设函数的一个属性 它包括参数θ0 θ1 θ2 在这幅图中 我画了一个训练集 我画了一组数据 让它更加可视化 但是 即使我们 去掉这个数据集 这条决策边界 和我们预测y等于1 与y等于0的区域 它们都是 假设函数的属性 决定于其参数 它不是数据集的属性

非线性决策边界,甚至是更复杂的边界（只要参数够多，比如多项、多元参数），举例如下：

2.3 损失函数 cost function

我们不能使用与线性回归相同的成本函数，因为logistic函数会导致输出波动，导致许多局部最优。换句话说，它不是凸函数。
以下面方式编写成本函数可以保证逻辑回归的j（θ）是**凸**的：

如果我们的正确答案“y”是1，那么如果我们的假设函数输出1，那么成本函数将是0。
如果我们的假设接近于0，那么成本函数将接近无穷大。

如果我们的正确答案“y”为0，那么如果我们的假设函数也输出0，那么成本函数将为0。
如果我们的假设接近1，那么成本函数将接近无穷大。

2.4 损失函数简化版

2.5 梯度下降

梯度下降的计算，线性回归和逻辑回归的区别只在于h(theta)

Welcome to MyBlog! This article was writed to take note my study of Machine Learning on Cousera.

---

1. 单元 线性回归模型 linear regression

h表示映射关系

1.1 代价函数

模型所预测的值与训练集中实际值之间的差距（下图中蓝线所指）就是建模误差（modeling error）

为了选出使得modeling error的平方和最小的模型参数。即代价函数：

1.2 梯度下降

一种有效的算法，能够自动找出使代价函数J取最小值的参数θ0和θ1.

2. 多元线性回归

2.1 多元线性回归的向量形式

转换成向量形式，如下：

2.2 用梯度下降解决多特征的线性回归问题

3. 特征缩放

3.1 缩放目的

这个问题有多个特征 如果你能确保这些特征 都处在一个相近的范围 我的意思是确保 不同特征的取值 在相近的范围内
下面举一个反面例子：

假如你有一个具有两个特征的问题 其中 x1 是房屋面积大小 它的取值 在0到2000之间 x2 是卧室的数量 可能这个值 取值范围在1到5之间 如果你画出代价函数 J(θ) 的轮廓图

3.2 缩放（特征缩放其实并不需要太过准确，只是为了加速梯度下降）

1. 不用过于担心 你的特征是否在完全 相同的范围或区间内 
但是只要他们都 只要它们足够接近的话 梯度下降法就会正常地工作

2. 均值规范化处理
其中，S为标准差（实际上，用最大值-最小值也是可以的），miu为均值

4. 学习率alpha的选择

通过损失函数的图像判断

5. 特征 和 多项式回归（polynomial regression）【和多元相对应】

5.1 选择特征的方法

有时 通过定义 新的特征 你确实会得到一个更好的模型 与选择特征的想法

We can combine multiple features into one. For example, we can combine x1 and x2 into a new feature x3 by taking x1⋅x2.

以预测房价为例 假设你有两个特征 分别是房子临街的宽度和垂直宽度 这就是我们想要卖出的房子的图片 临街宽度 被定义为这个距离 其实就是它的宽度 或者说是 你拥有的土地的宽度 如果这块地都是你的的话 而这所房子的 纵向深度就是 你的房子的深度 这是正面的宽度 这是深度 我们称之为临街宽度和纵深 你可能会 像这样 建立一个 线性回归模型 其中临街宽度 是你的第一个特征x1 纵深是你的第二个 特征x2 但当我们在 运用线性回归时 你不一定非要直接用 给出的 x1 和 x2 作为特征 其实你可以自己创造新的特征 因此 如果我要预测 房子的价格 我真正要需做的 也许是 确定真正能够决定 我房子大小 或者说我土地大小 的因素是什么 因此 我可能会创造一个新的特征 我称之为 x 它是临街宽度与纵深的乘积 

5.2 如何得到不同的学习算法

如何将一个 多项式 如一个二次函数 或一个三次函数拟合到你的数据

Our hypothesis function need not be linear (a straight line) if that does not fit the data well.
We can change the behavior or curve of our hypothesis function by making it a quadratic, cubic or square root function (or any other form).

6. 正规方程

对于某些线性回归问题 它给出了一个更好的方法 求出参数 θ 的最优解
相对于梯度下降一步步求到最优解，正规方程法，提供了一种求theta的解析接发，可以一次性求解theta的最优解

6.1 正规方程直观理解

6.2 如何选择梯度下降 和 正规方程法(只适用于线性回归)

只要特征变量的数目并不大 正规方程是一个很好的 计算参数 θ 的替代方法 具体地说 只要特征变量数量小于一万 具体地说 只要特征变量数量小于一万 我通常使用正规方程法 我通常使用正规方程法 而不使用梯度下降法

6.3 正规方程的不可逆性

当你发现的矩阵X'X的结果是奇异矩阵 或者找到的其它矩阵是不可逆的 我会建议你这么做 首先 看特征值里是否有一些多余的特征