Welcome to MyBlog! This article was writed to take note my study of Machine Learning on Cousera.
卷积运算
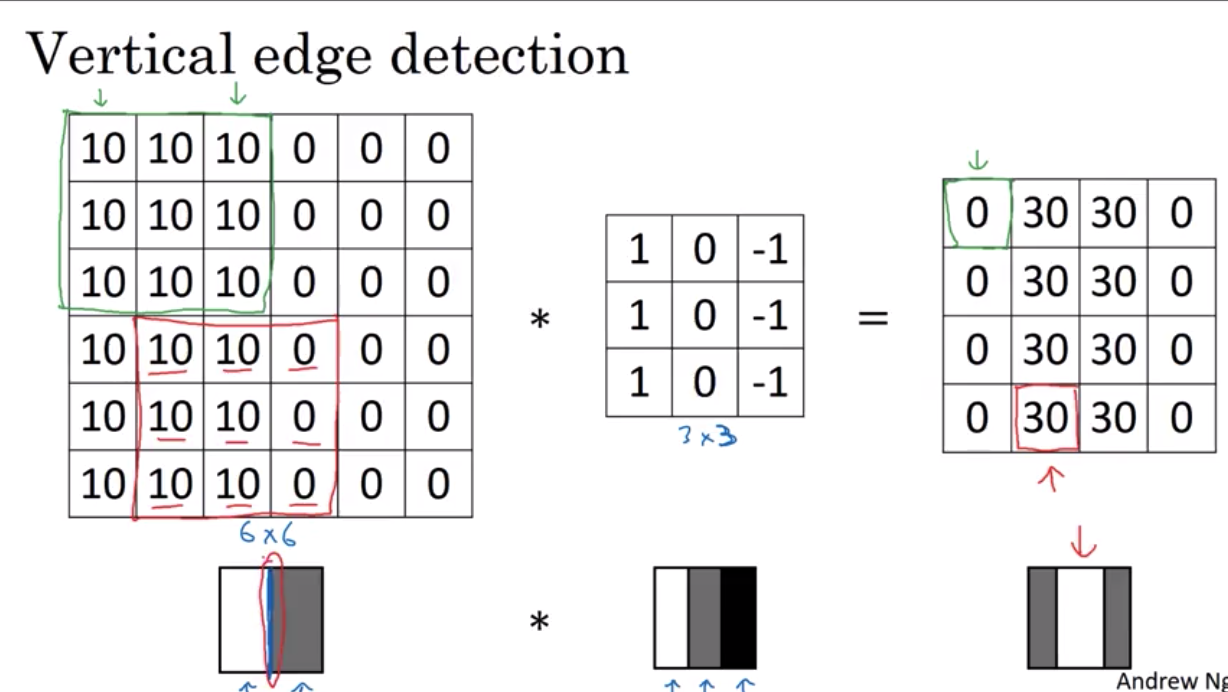
vertical edge detection
总之 将这9个数字当成参数去学习 是计算机视觉里的一个有用的想法
padding 补白/填充
为了构建深层神经网络,一个你非常需要使用的,对基本的卷积操作的改进是填充(padding)
通常在计算机视觉(computer vision)领域 f基本上是使用奇数 事实上几乎永远是奇数
并且你很少看到偶数大小的 计算机视觉使用的过滤器 并且我想有两个原因导致这个现象 一是如果f是偶数 你会需要一些不对称的填充 所以只有当f是奇数时 这种same卷积会产生 在四周有相同的维度的一个自然的填充区域 而不是在左边多填充在右边少填充 或者别的不对称的填充 其次当你有一个奇数大小的过滤器 比如3x3或者5x5 这样这可以有一个中心位置 有时候在计算机视觉领域 有一个特殊点是很好的 有一个这样的像素是很好的 你可以称之为中心像素 这样你就可以描述你过滤器的位置 也许这些都不是
为什么f基本上永远使用奇数的很好的理由 但是如果你去读一些卷积相关的文献 你会发现3x3的过滤器非常常见 你会看见一些5x5,7x7 事实上有时候 之后我们会讲到1x1过滤器和它的原理 但是只是约定俗成 我建议你也使用奇数大小的过滤器 我想就算你使用一个偶数f 你也许能得到不错的结果 但是如果你坚持计算机视觉的传统 我一般只用奇数f
你可以只说这是一个valid卷积 意味着p=0 或者你可以说这是一个same卷积
意味着使用足够的填充 使得输出输入的大小相等 所以这就是填充
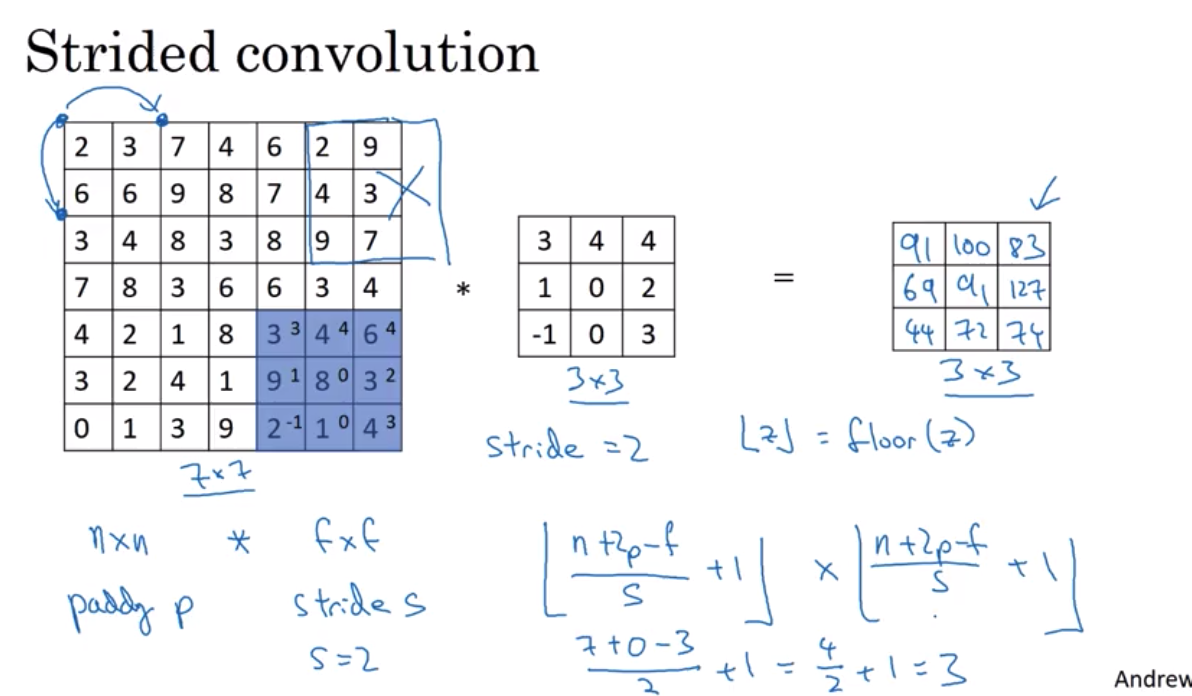
在下一个视频,让我们来讲讲如何实现步幅(stride)卷积strided convolutions 带步长的卷积
输入和输出的维度间的关系可以用以下的方程进行表示 如果你有一个NxN大小的图像 用一个FxF大小的过滤器对这个图像进行卷积 对图像使用p层填充,并假设步长为S。
如果这个分数中,分子不能被分母整除得到整数怎么办? 这时,我们可以向下取整 用这个标志表示对于某个值向下取整 这又叫floor(z) 它表示最接近z的小于z的整数 之所以这样,是因为 蓝色区域被像素或补充的元素填满时,得到的是正数 如果蓝色区域 部分没有被图像或图像加填充部分覆盖 就这样落在外部的时候,我们不能进行计算 这说明,3X3的过滤器 必须全部落在原图像 或原图像加上填充的范围之内 就形成了这样的约定 之后,计算输出维度的正确做法是 如果(N+2P-F)/S不是整数的话,则将其向下取整。
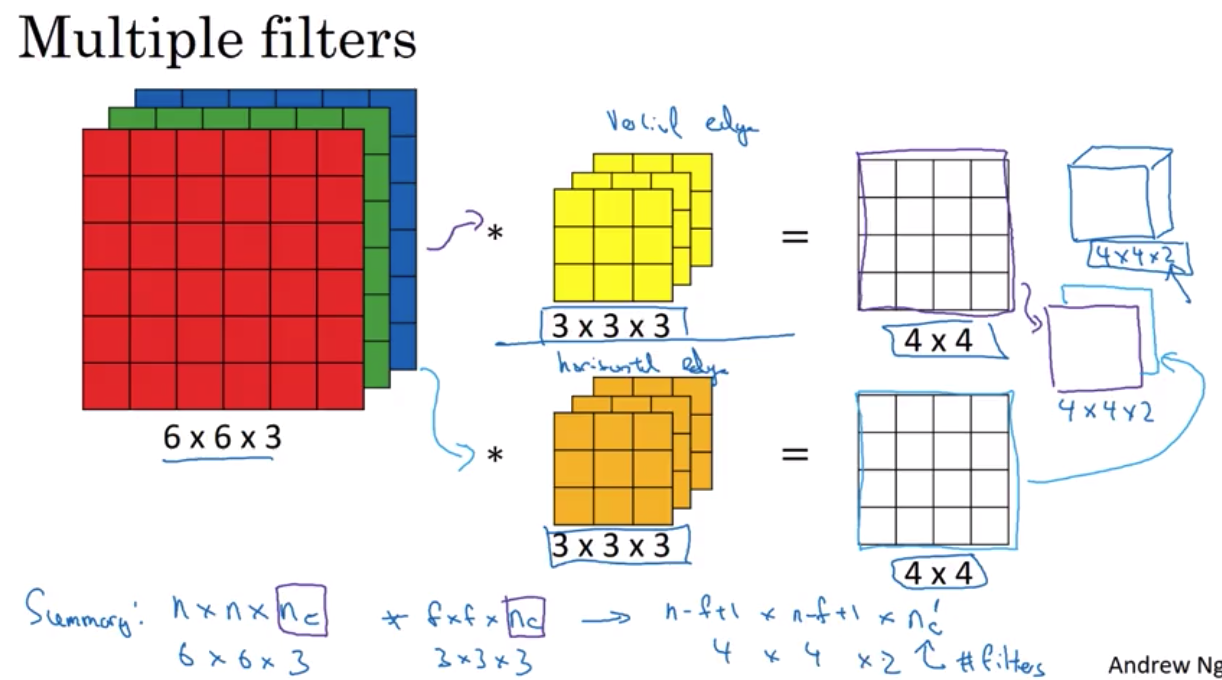
convolutions over volume
你会得到一个 n-f+1 乘以 n-f+1乘以这边的nc’, 或者说下一层的nc, 也就是你所用的过滤器的数量。
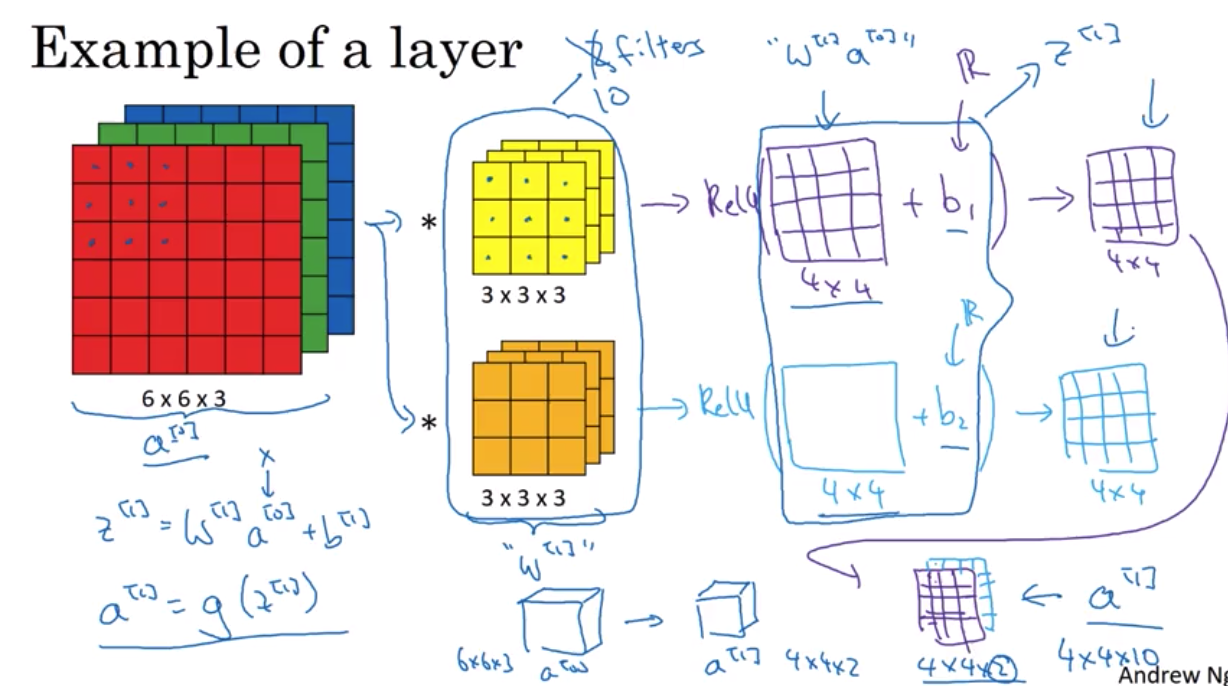
one layer of a convolutional network
这个特征使得卷积神经网络 不太容易过拟合(overfitting)
现在想象一下 前面我们的图中是两个过滤器 现在这里我们有10个过滤器 1, 2, … 10个 加起来是28x10 也就是280个参数 注意这里. 一个很好的特性是. 不管输入的图像有多大 比方1000 x 1000 或者5000 x 5000, 这里的参数个数不变. 依然是280个 因此 用这10个过滤器来检测一个图片的不同的特征,比方垂直边缘线, 水平边缘线 或者其他不同的特征 不管图片多大 所用的参数个数都是一样的
simple convolutional network example
pooling
这里只有这些超参需要你设定一次 或许是人工设定或者使用交叉检验
除此之外,你就不用做什么了 它就是一个神经网络在其中一层计算的确定函数
而这里实际上没有任何需要学习的 它仅仅是一个确定的函数max pooling
如果你把这个4x4的区域看作某个特征的集合 即神经网络某个层中的激活状态 那么 一个大的数字 意味着它或许检测到了一个特定的特征 所以 左侧上方的四分之一区域有这样的特征 它或许是一个垂直的边沿 亦或一个更高或更弱 显然 左侧上方的四分之一区域有那个特征 然而这个特征 或许它不是猫眼检测 但是 右侧上方的四分之一区域没有这个特征 所以 max pooling做的是 检测到所有地方的特征 四个特征中的一个被保留在max pooling的输出中 所以,max pooling作所做的其实是 如果在滤波器中任何地方检测到了这些特征 就保留最大的数值 但是 如果这个特征没有被检测到 可能左侧上方的四分之一区域就没有这个特征 于是 那些数值的最大值仍然相当小 这或许就是max pooling背后的解释
pooling的一个有趣的特性是 它有一套超参 但是它没有任何参数需要学习 实际上
没有任何需要梯度相加算法学习的东西 一旦确定了 f 和 s 就确定了计算
而且梯度下降算法不会对其有任何改变 average pooling
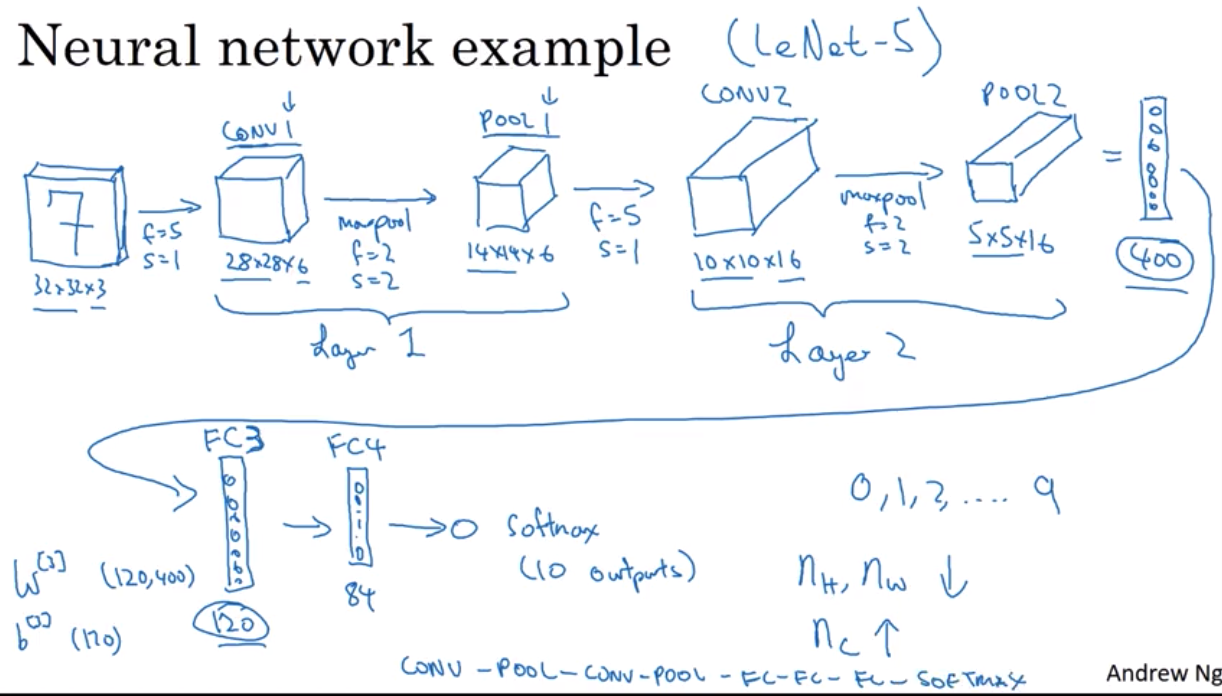
CNN Example
神经网络中当人们说到网络层数的时候,通常指 那些有权重,有参数的网络层数量 因为池化层没有权重,没有参数 只有一些超参数,我会使用 卷积层1和池化层1为一体的说法 把他们作为层一,尽管有时候 当你看在线文章或读研究论文时,你会听到卷积层 和池化层被称为两个独立层 但这不过是二种细微不一致的表示术语 这里当我计算层数,我只会算那些有权重的层 所以我视这二个一起为层一 并且Conv1和Pool1名字末尾是1 也表明了我认为二者都是神经网络层一的组成部分
关于如何选择这类超参数 也许一个常用的法则实际上是 不要试着创造你自己的超参数组 而是查看文献,看看其他人使用的超参数 从中选一组适用于其他人的超参数 很可能它也适用于你的应用
why convolutions?
如果你是创建一个一层有3072个单元的神经网络 下一层是4704个单元 然后你会连接每一个这些神经元 接着是权重矩阵 在权重矩阵,这些参数的总数是3072 乘以4704,结果大约是1400万个 所以这样就有很多参数需要训练 当然如今你可以训练比1400万更多参数的神经网络 但是,考虑到这仅仅是很小的图像 却有如此多的参数需要训练 而且,如果说有一个1000×1000的图像 那么这个权重矩阵将会变得非常大 但是如果你看看这个卷积层的参数总数 每个滤网是5x5 因此每个滤网有25个参数 而且一个偏置参数对每个滤网会错过26个参数 你有6个滤网 所以总共的参数总数 就等于156个参数 所以这个卷积层的参数总数仍然很少
相比于全链接层,卷积的参数会少很多很多
卷积神经网络参数很少的原因有两个 一个是参数共享 用相同的9个参数来计算所有16个输出结果 是减少参数个数的方法之一 而且,直观的来看,像垂直的边缘探测器 这类功能探测器来计算它图片的左上角 相同的特征可能会在后面有用处 当用在右下角,这个特征有可能也会有用
另一个是稀疏式联系第二种卷积神经网络避免 只有相对少的参数方法是建立稀疏的联系 我的意思是 如果你看着这个0 这个是通过一个3×3的卷积算出来的 所以,它只是根据这个3×3格子的输入来决定的 所有这个右边输出单元 只和这个9分之36 (6×6=36)个特征所相连 以及所有剩下的像素(格子)值 这个像素值对其他输出值没有任何的影响 这就是我所说的稀疏式联系
卷积神经网络会被用来捕捉平移不变 我们可以观察到 一张猫的图片,它的像素格从右边移动了几格 还是一个非常清晰的猫的图片 卷积结构帮助神经网络编译了 当一张图面移动了几个像素格,它同样还应该产生非常相似的特征 应该给它一个相同的标签 同时,因为你使用了相同的滤网 这张图片的各个部分 平移之前和平移之后的图层 帮助神经网络自然而然地学会更稳定 或者更佳的捕捉到平移不变所需要的特性