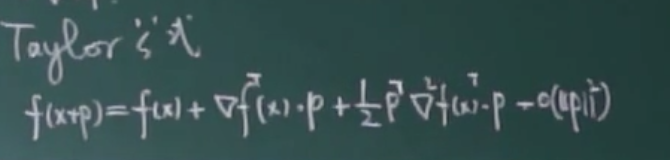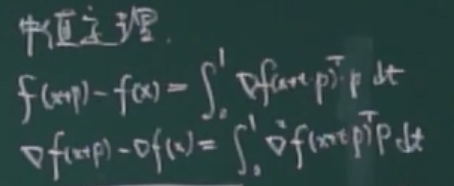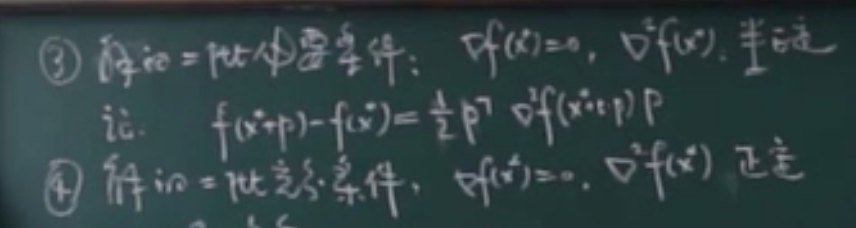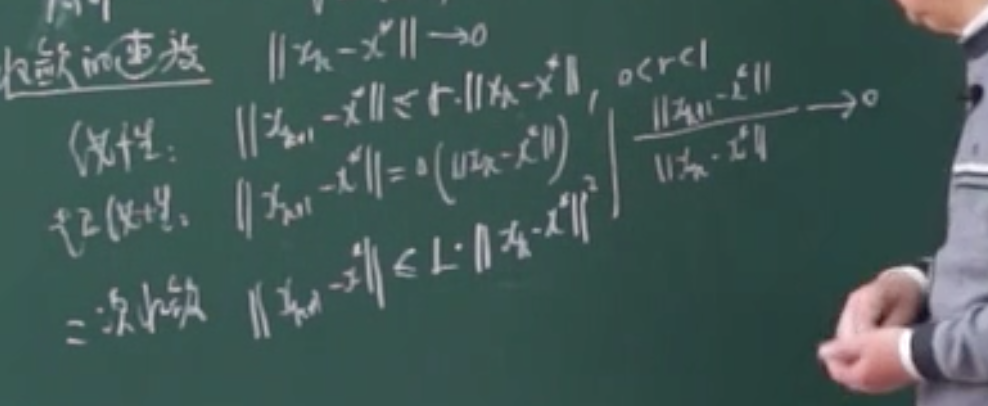Welcome to MyBlog!
该博客内容是在观看了吴立德老师的数值优化课程记录下的一些笔记,仅供个人复习所用。课程传送门
1. “解”的概念 x🌟
2. 解的条件
2.1 taylor公式,n元多项式
2.2 中值定理
2.3 一阶必要条件
反证法,忘记了可以回顾视频2.4 二阶必要条件(半正定
矩阵A正定是指,对任意的X≠0恒有X^TAX>0
矩阵A半正定是指,对任意的X≠0恒有X^TAX≥02.5 二阶充分条件(正定)
2.6 凸函数的解
3. 算法
3.1 概念
迭代算法: x0->x1->….->xi->xi+1, x最后收敛到我们要的解
算法就是怎么从xi,求出下一个迭代点xi+1
一定包含终止条件:||∇f(xi)|| -> ||∇f(x🌟)||=0时必要条件
或者: f(x+1)-f(x)差值比较小
3.2 直接、一阶、二阶 方法
3.3 算法的收敛性
3.3.1 全局收敛的算法
3.3.2 局部收敛的算法
3.4 算法的收敛速度
线性收敛、超线性收敛(超线性其实就是线性收敛里面r趋紧于0)、二次收敛(牛顿收敛就是二次收敛)3.5 方法
线性搜索方法
信赖域方法
·
3.5.1 线性搜索方法
x(k), 选一个方向p(k),在选一个步长a(k)
x(k+1) = x(k) + a(k)*p(k)
(1)选方向
- 最速下降法(梯度方向)(一阶)
- 牛顿方向 (只有在铁的附近在回快,而且对计算机内存要求很高)
- 拟牛顿方向 (即保存了收敛的速度,又不想要计算二阶导数)
- 共轭梯度法