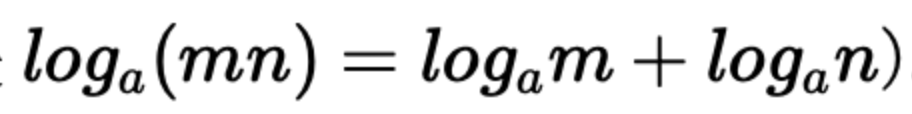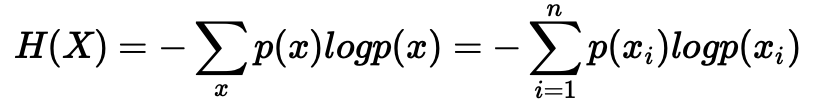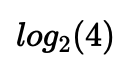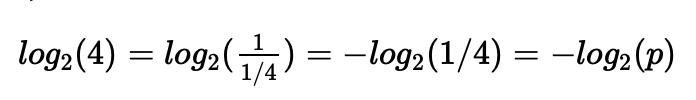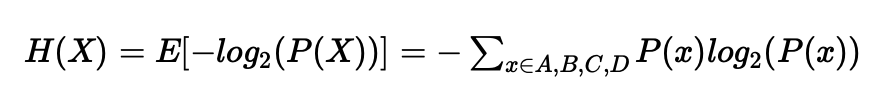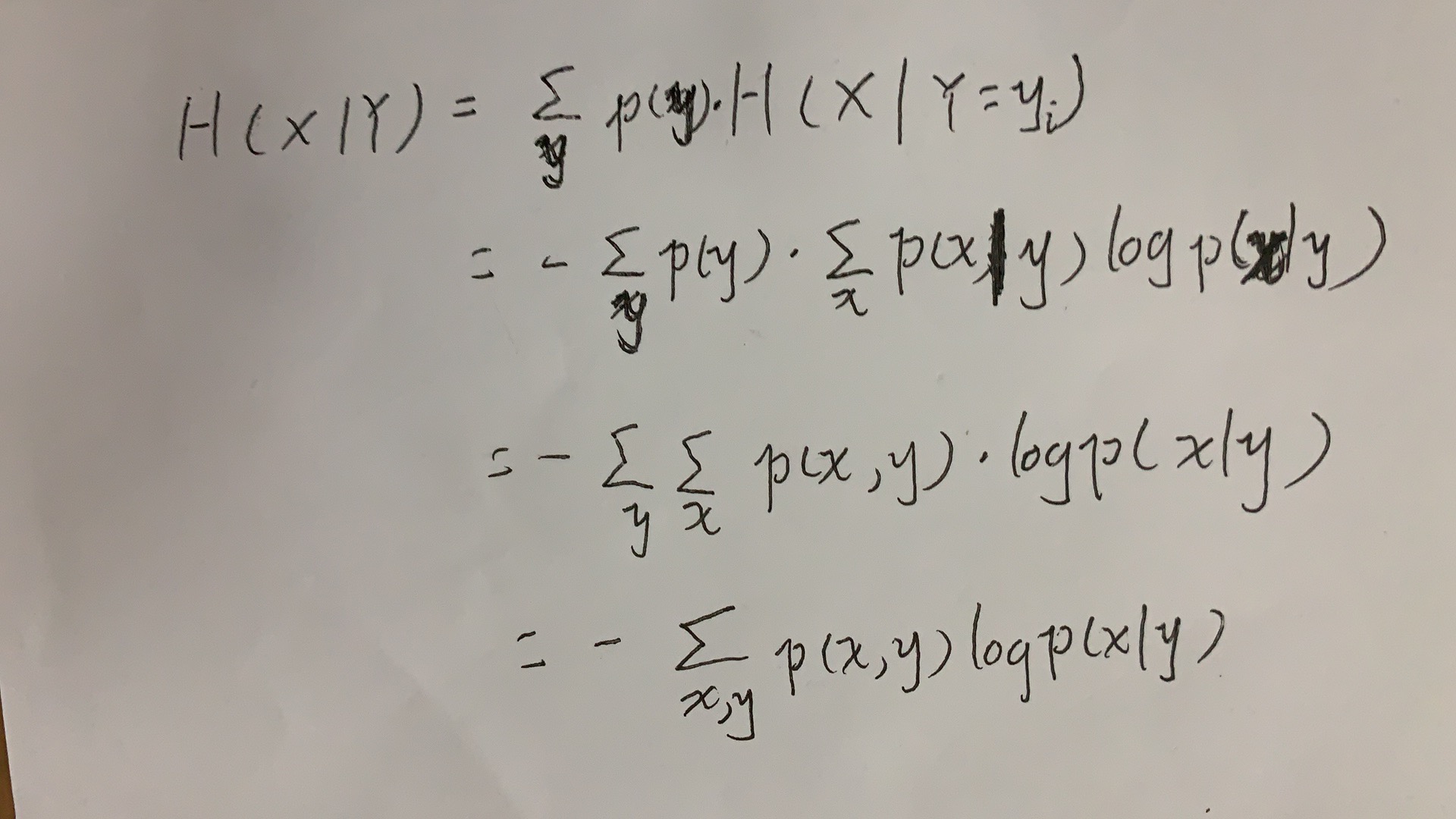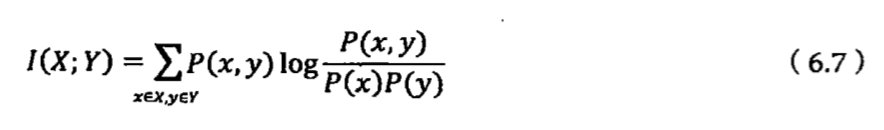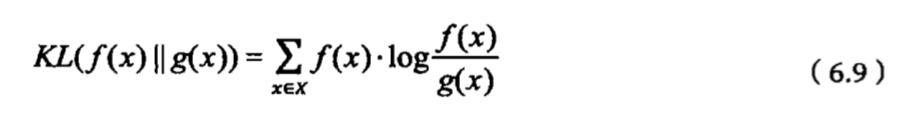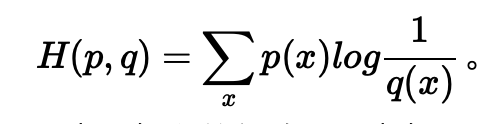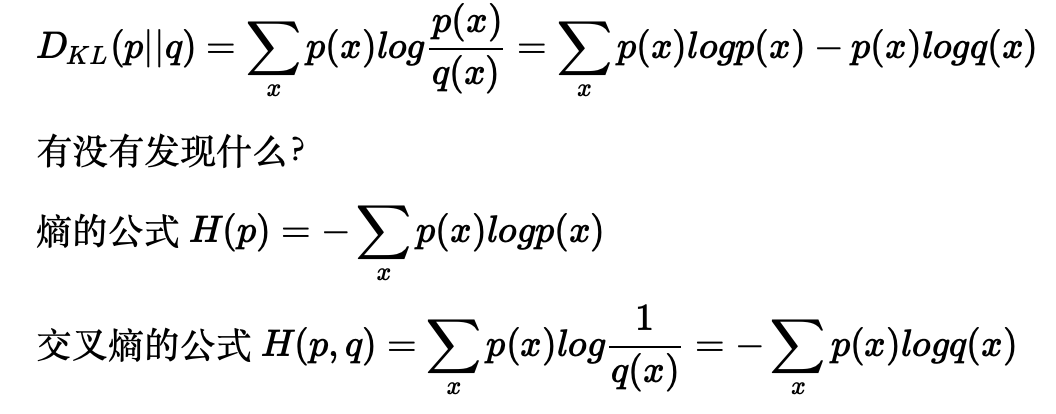Welcome to MyBlog!
信息熵
信息熵的概念
信息熵公式的理解
自信息
引入一个新的概念:自信息:用来衡量某个具体变量或者事件具体发生时,包含的信息量。在这里我们用I(X)表示
如果我们有两个不相关的事件 x 和 y,那么观察两个事件同时发生时获得的信息量应该等于观察到事件各自发生时获得的信息之和,即:I(x,y)=I(x)+I(y)。
因为两个事件是独立不相关的,因此 p(x,y)=p(x)p(y)。根据这两个关系,很容易看出 I(x)一定与 p(x)的对数有关 (因为对数的运算法则是
因此,我们有I(x)=−logp(x)其中负号是用来保证信息量是正数或者零。而 log 函数基的选择是任意的(信息论中基常常选择为2,因此信息的单位为比特bits;而机器学习中基常常选择为自然常数)
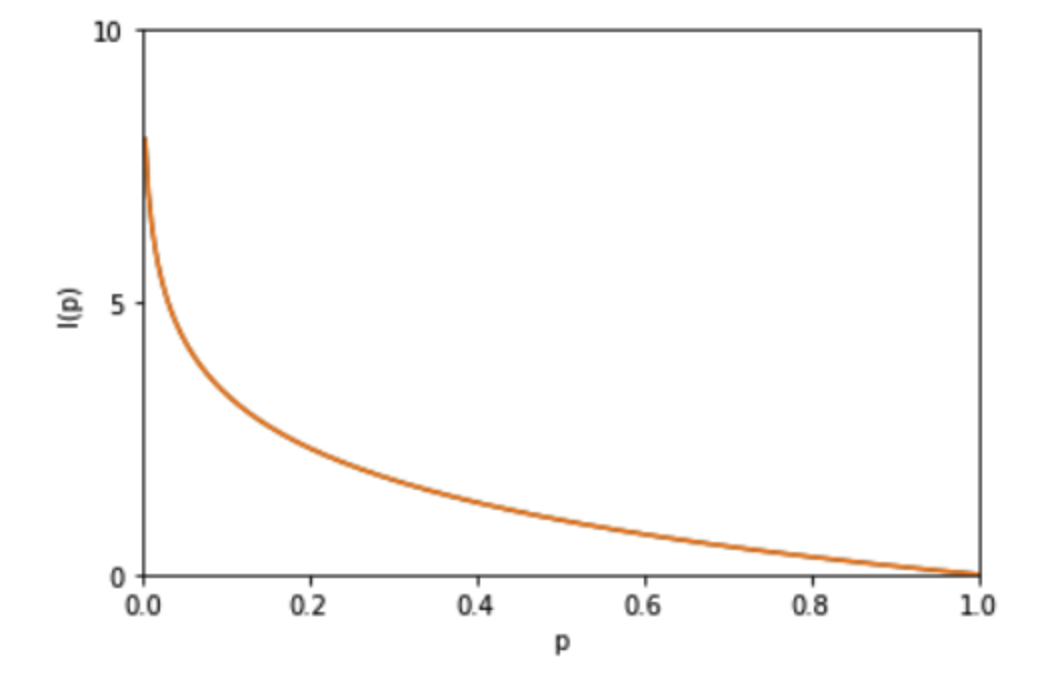
I(x)描述的是随机变量的某个事件发生所带来的信息量。图像如图:
信息熵的数学表示
自信息和信息熵的对比:自信息只能处理单个的输出。而熵是对整个概率分布中不确定性总量进行量化
现在假设一个发送者想传送一个随机变量的值给接收者。那么在这个过程中,他们传输的平均信息量可以通过求 I(x)=−logp(x)关于概率分布 p(x)的期望得到,即:
从公式可得,随机变量的取值个数越多,状态数也就越多,信息熵就越大,混乱程度就越大。当随机分布为均匀分布时,熵最大,且 0≤H(X)≤logn
熵和编码长度
信息论中,熵代表着根据信息的概率分布,对信息的编码,所需要的最短平均编码长度。
举个简单的例子来理解一下这件事情:假设有个考试作弊团伙,需要连续不断地向外传递4选1单选题的答案。直接传递ABCD的ascii码的话,每个答案需要8个bit的二进制编码,从传输的角度,这显然有些浪费。信息论最初要解决的,就是数据压缩和传输的问题,所以这个作弊团伙希望能用更少bit的编码来传输答案。很简单,答案只有4种可能性,所以二进制编码需要的长度就是取2为底的对数:
此时已经有些像熵的定义了。回顾一下熵的定义,正是求−log(p)的期望值,所以我们把这个思路也套用一下:
信息的作用
概述
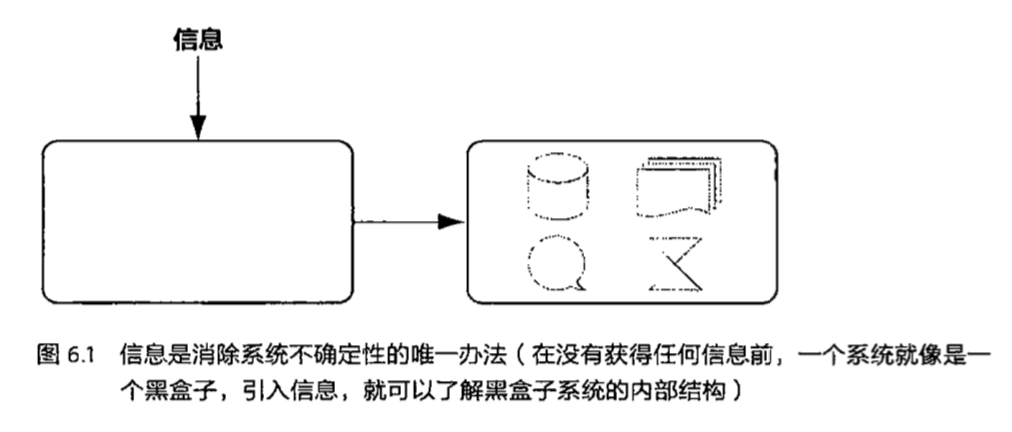
一个事物内部存在着随机性,也就是不确定性,假定为U,而外部消除这个不确定性唯一的办法就是引入信息I,而需要引入的信息量取决于这个不确定性的大小,即I>U才行。当I<U时间,这些信息可以消除一部分不确定,也就是新的不确定性。
反之,如果没有信息,任何公式或者数字的游戏都无法排除不确定性。
案例
直接信息和相关信息,都可以降低随机事件的不确定性。
条件熵
条件熵的概念
为什么“直接的、相关的”信息也能过消除不确定性?怎么判断信息是相关的还是直接的或者是无关信息? 为此,需要引入一个概念:条件熵、互信息
只要证明 H(X)>=H(X|Y) ,也就说明了多了Y的信息后,关于X的不确定性下降了。
公式的理解
条件熵 H(X|Y) 定义为:Y给定的条件下,X对Y的条件概率的信息熵,对Y的数学期望:
互信息
互信息的引入
这里引入另一个概念:“互信息”是作为两个随机事件“相关性”的量化度量。
当x和y完全相关时,它的取值是1;当二者完全无关时,它的取值是0;
互信息的具体应用
相对熵
概念
相对熵也是用来衡量相关性,但是和随机变量的互信息不同,它是用来衡量两个取值为正数的函数的相关性。