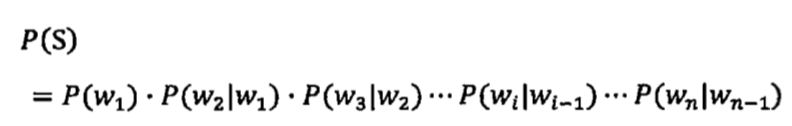1. 统计语言模型的提出
1.1 20世纪70年代以前
统计语言模型产生初衷就是为了解决语言识别问题。
一个语音识别系统,听到一下句子:The apple and 「pear」 salad is delicious.
系统它应该如何翻译:The apple and 「pear」 salad is delicious.
还是:The apple and 「pair」 salad is delicious.(pear和pair在英文里发音相同)科学家们解决以上问题,是通过判断这个文字序列是否合乎语法、含义是否正确。
1.2 20世纪70年代之后
贾里尼克从另外一个角度看待问题,用一个简单的统计模型非常漂亮地搞定了它。
他的想法是:一个句子是否合理,就看看他的可能性大小如何,至于可能性就用概率来衡量。比如上面的“苹果梨和沙拉很好吃”的语音问题,第一个句子出现的概率是10的-20次分,第二个句子出现的概率是10的-25次方。那么,第一个句子是最有可能的。
2. 统计语言模型的数学表示
2.1 贾里尼克提出了一个简单的统计模型
假定S表示某一个有意义的句子,由一串特定顺序排列的词w1,w2,w3….Wn构成的,这里n是句子的长度。那么P(S)就表示S在文本中出现的可能性。
只要把人类自诞生以来说过的话全部统计下,就知道这句话出现的概率了。但是这种方法显然是不可行。因此,需要一个模型来估算P(S)。
但是这里有一个问题,前面的词P(w1),P(w2)都很容易计算,但到了最后一个词Wn,P(Wn|W1,W2,W3,…,Wn-1)的可能性太多,无法估算
2.2 马尔可夫假设
他给出了一个方法,就是假设任意一个词Wt出现的概率只同他前面的词Wt-1有关,于是问题就变得很简单了。
2.2.1 计算过程
2.3 补充:N元模型、高阶模型
2.3.1 n元模型的概念
所谓n元模型,就是假设一个词由前面n-1个词决定。
所以在2.2中提到的马尔可夫假设,就是二元模型。
2.3.2 N一般取值都很小
主要有两个原因:
2.3.3 马尔可夫假设的局限性
在自然语言中,上下文之间的相关性可能跨度非常大,甚至一个段落跨越到另一个段落。三元、四元、甚至是更高阶的模型都不能覆盖所有的语言现象。
3. 模型训练
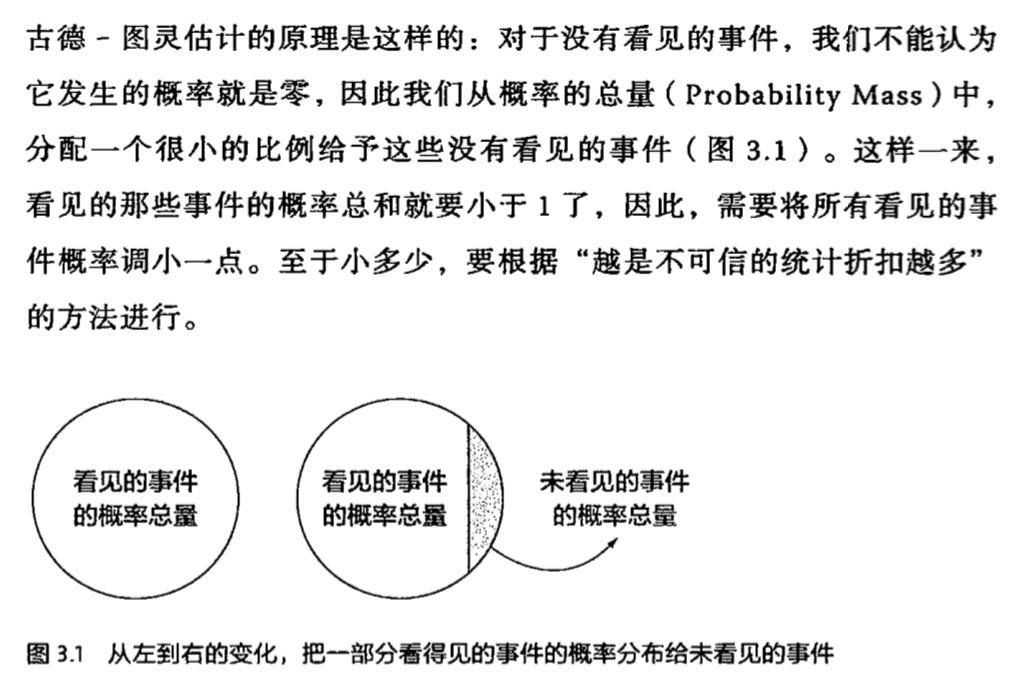
3.1 “不平滑”现象
3.1.1 原因:零概率和一概率
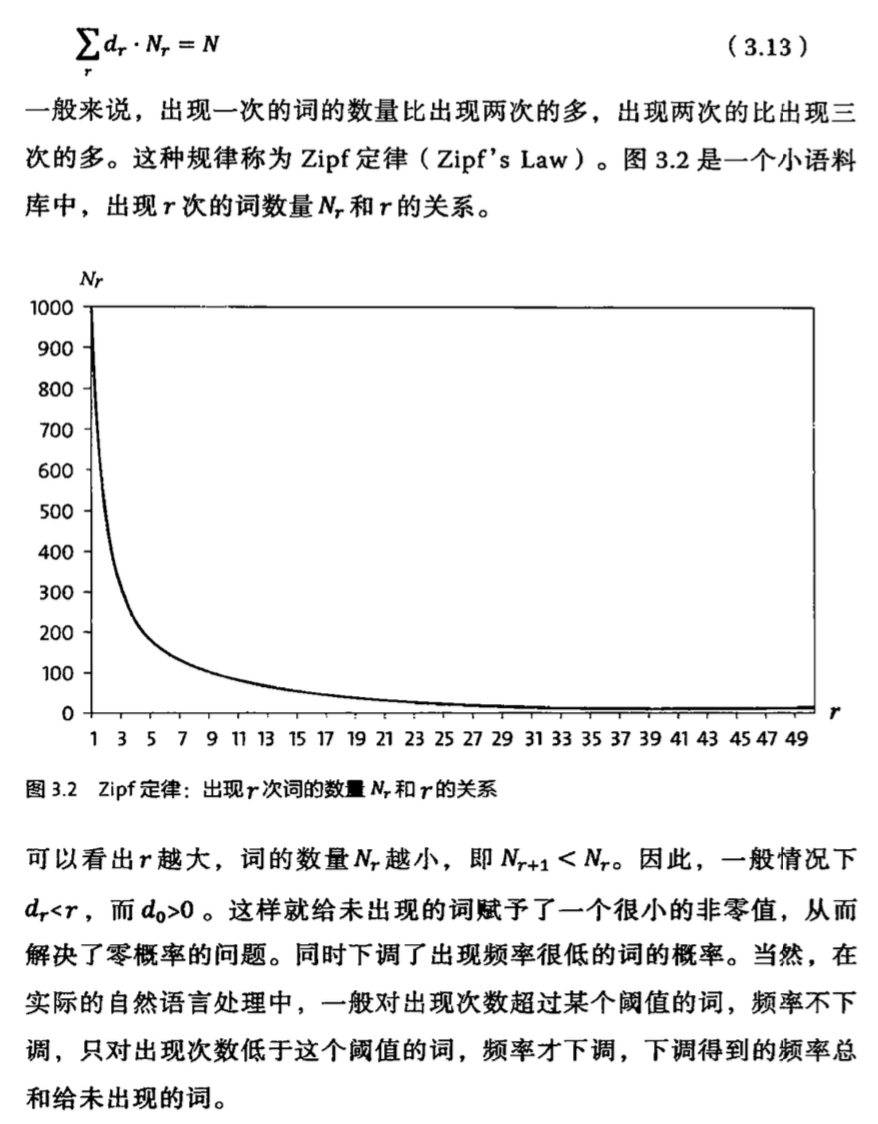
3.1.2 解决方法1: 卡茨退避法
3.1.3 解决方法2: 删除差值
3.2 语料选取
- 训练语料和模型应用的领域,不能相脱节
- 训练数据通常越多越好
- 在成本不高的情况下,过滤训练数据是需要的