Welcome to MyBlog! This article was writed to take note my study of Machine Learning on Cousera.
1. 用线性回归训练二分类器
原文:分类问题其实和回归问题类似
To attempt classification, one method is to use linear regression and map
all predictions greater than 0.5 as a 1 and all less than 0.5 as a 0.
However, this method doesn't work well because classification is not
actually a linear function
The classification problem is just like the regression problem.2. 逻辑回归 (sigmoid函数、逻辑函数、S函数 基本是同义词)
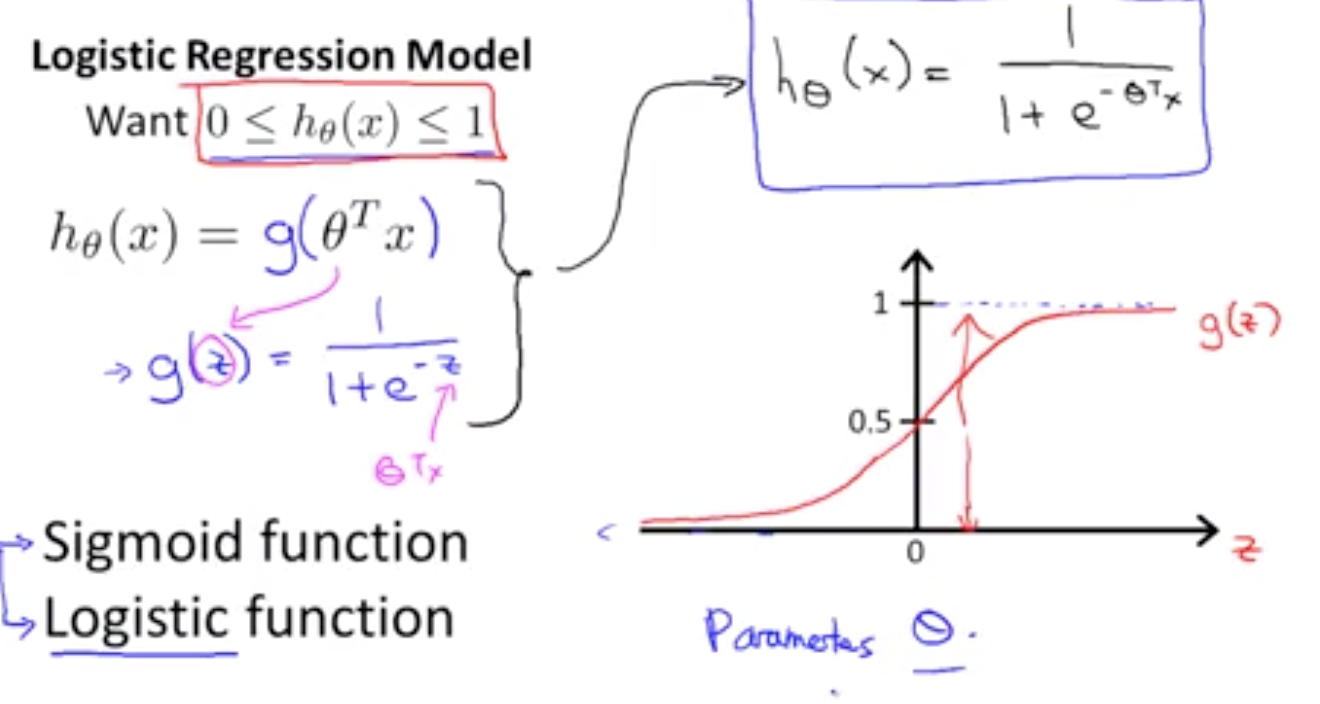
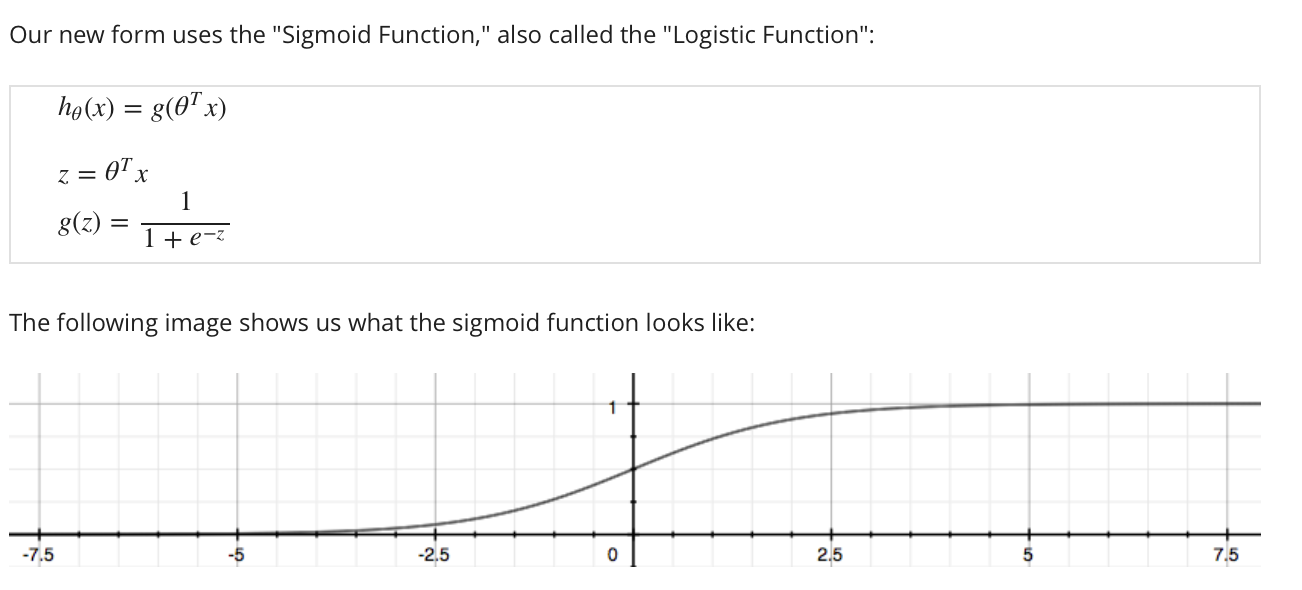
2.1 函数表示(假设函数)
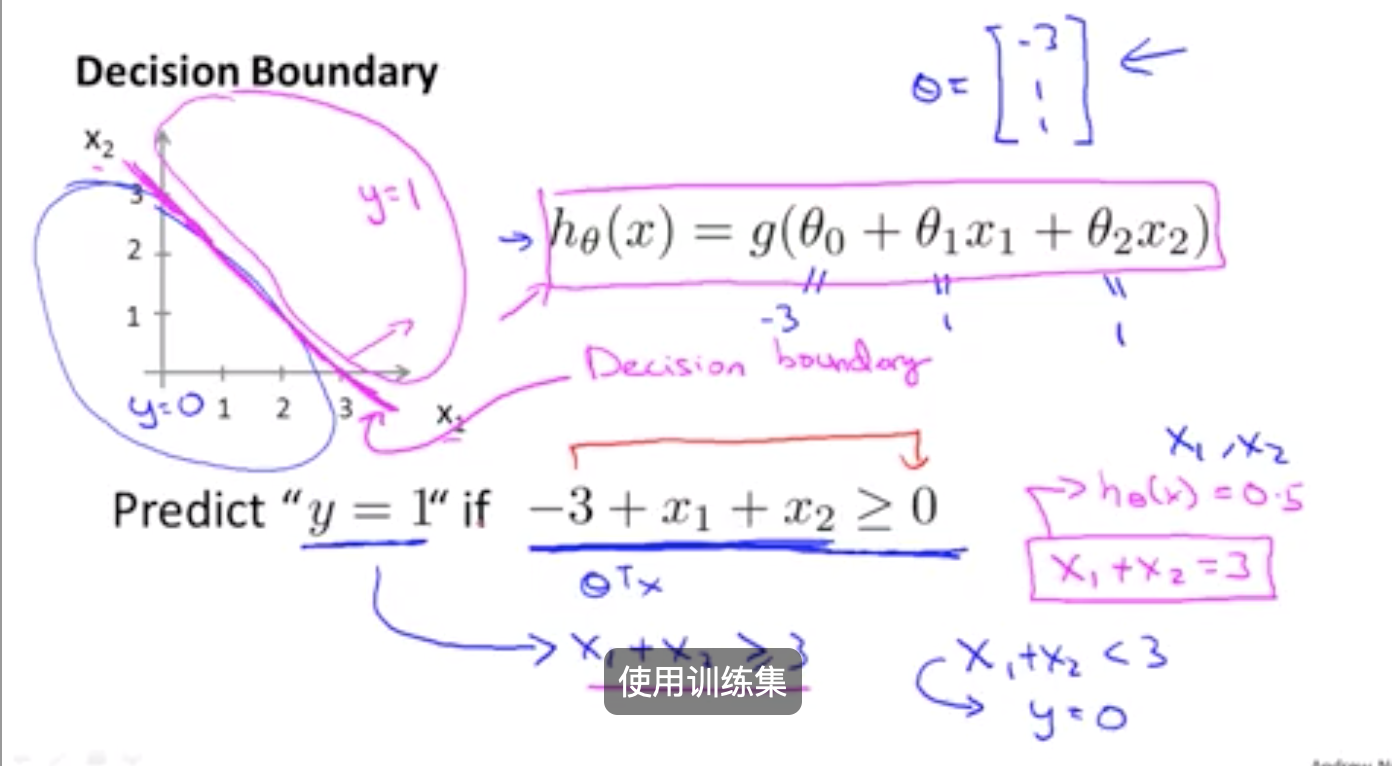
2.2 决策边界(decision boundary)
决策边界是 假设函数的一个属性 它包括参数θ0 θ1 θ2 在这幅图中 我画了一个训练集 我画了一组数据 让它更加可视化 但是 即使我们 去掉这个数据集 这条决策边界 和我们预测y等于1 与y等于0的区域 它们都是 假设函数的属性 决定于其参数 它不是数据集的属性
非线性决策边界,甚至是更复杂的边界(只要参数够多,比如多项、多元参数),举例如下:
2.3 损失函数 cost function
我们不能使用与线性回归相同的成本函数,因为logistic函数会导致输出波动,导致许多局部最优。换句话说,它不是凸函数。
以下面方式编写成本函数可以保证逻辑回归的j(θ)是**凸**的:
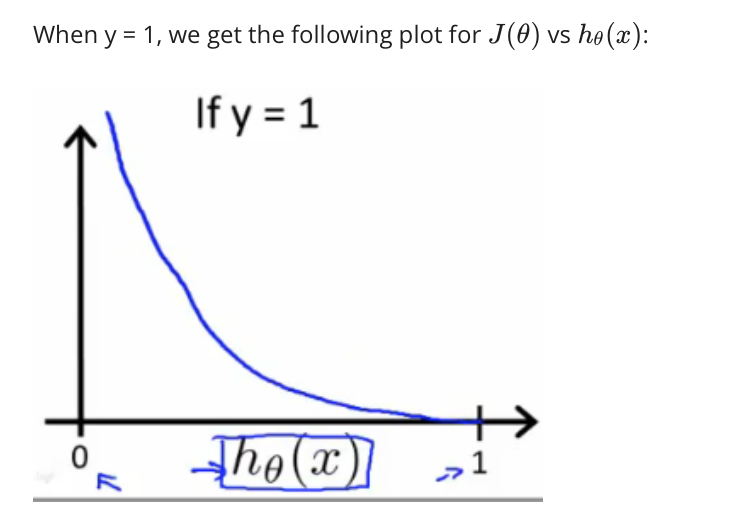
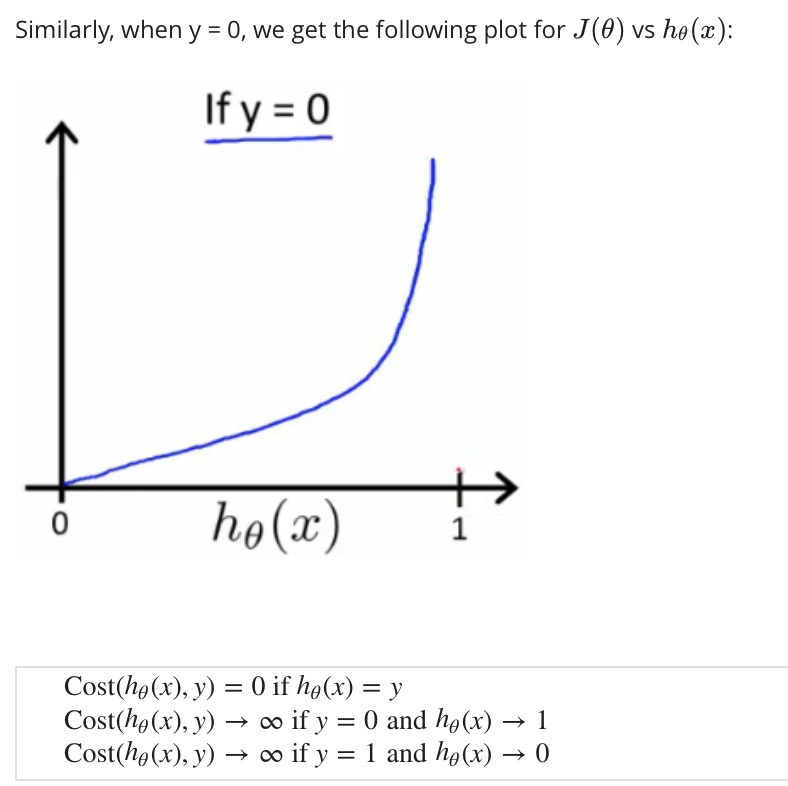
如果我们的正确答案“y”是1,那么如果我们的假设函数输出1,那么成本函数将是0。
如果我们的假设接近于0,那么成本函数将接近无穷大。如果我们的正确答案“y”为0,那么如果我们的假设函数也输出0,那么成本函数将为0。
如果我们的假设接近1,那么成本函数将接近无穷大。2.4 损失函数简化版
2.5 梯度下降
梯度下降的计算,线性回归和逻辑回归的区别只在于h(theta)