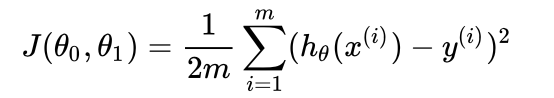Welcome to MyBlog! This article was writed to take note my study of Machine Learning on Cousera.
1. 单元 线性回归模型 linear regression
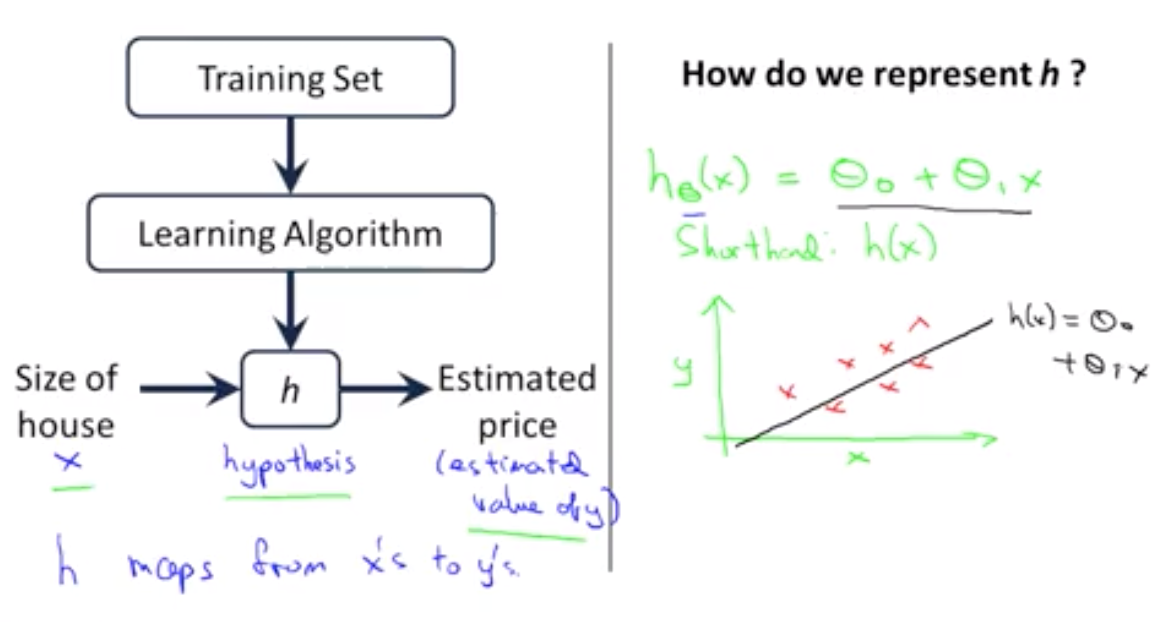
h表示映射关系
1.1 代价函数
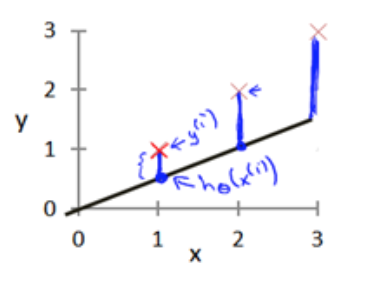
模型所预测的值与训练集中实际值之间的差距(下图中蓝线所指)就是建模误差(modeling error)
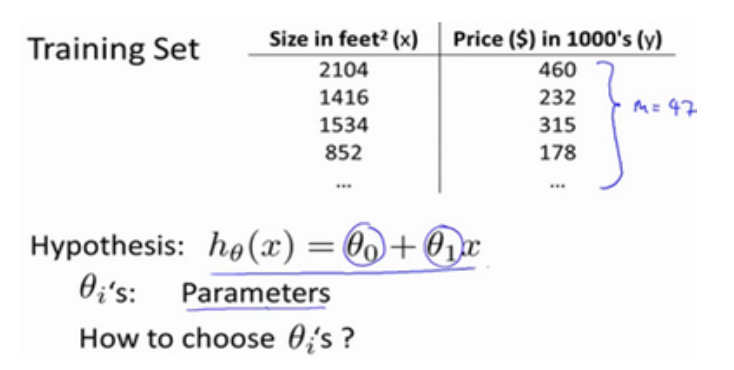
为了选出使得modeling error的平方和最小的模型参数。即代价函数:
1.2 梯度下降
一种有效的算法,能够自动找出使代价函数J取最小值的参数θ0和θ1.
2. 多元线性回归
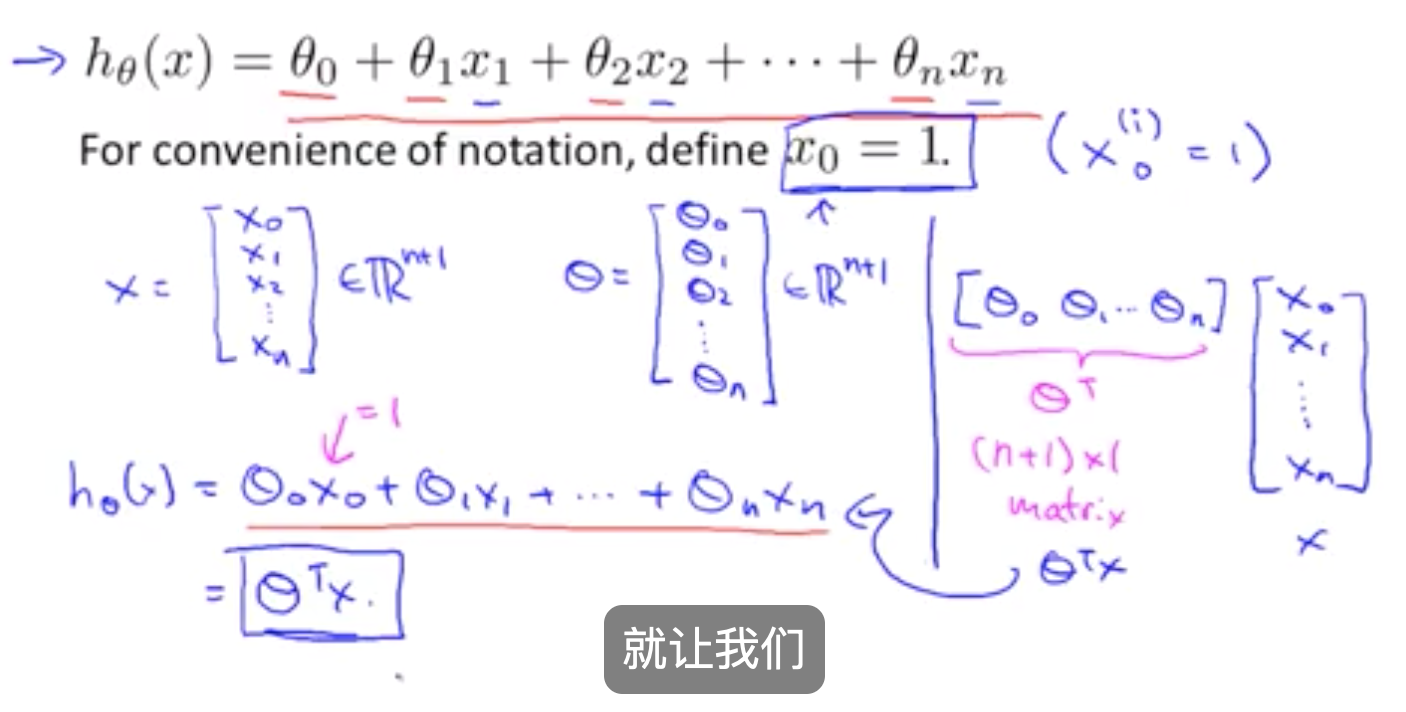
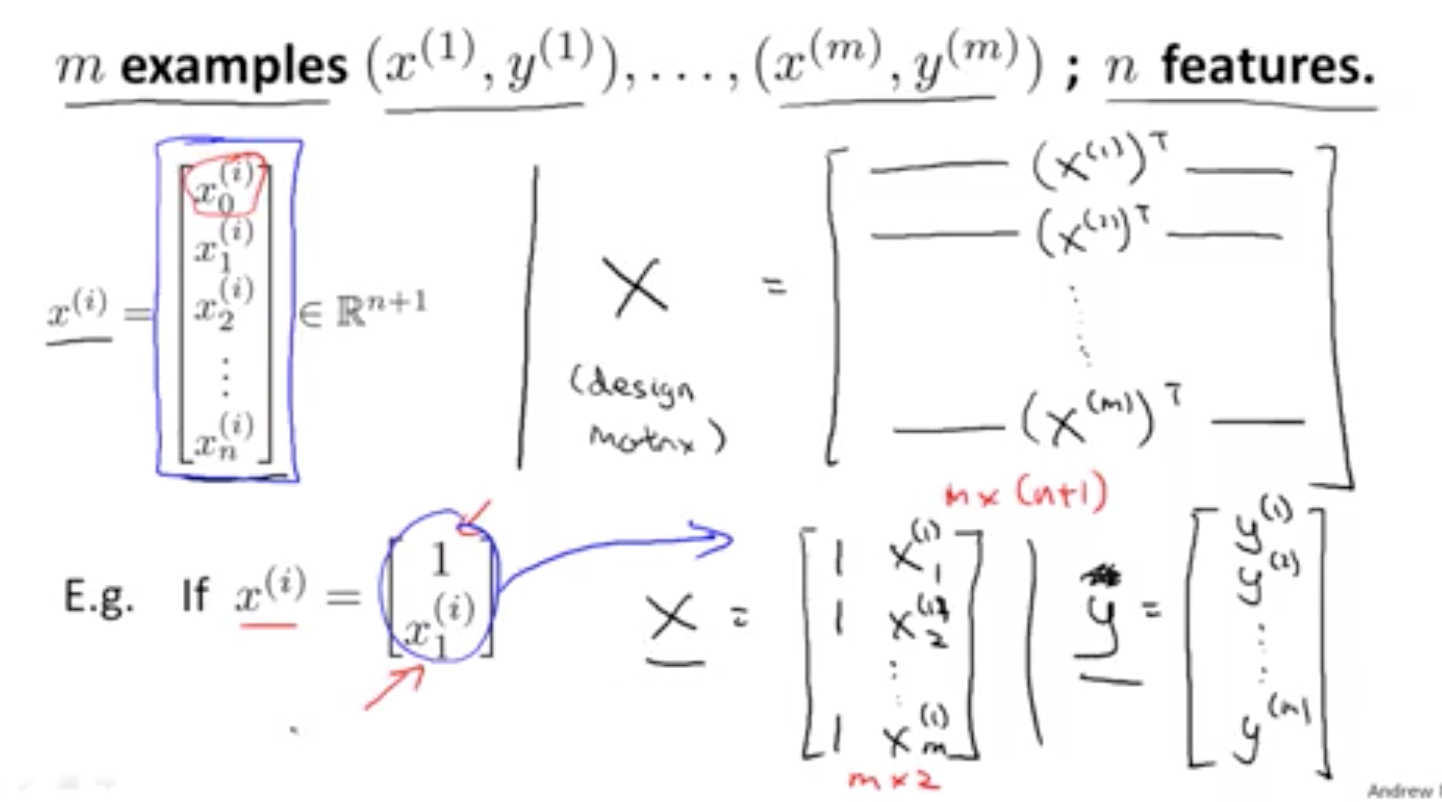
2.1 多元线性回归的向量形式
转换成向量形式,如下:
2.2 用梯度下降解决多特征的线性回归问题
3. 特征缩放
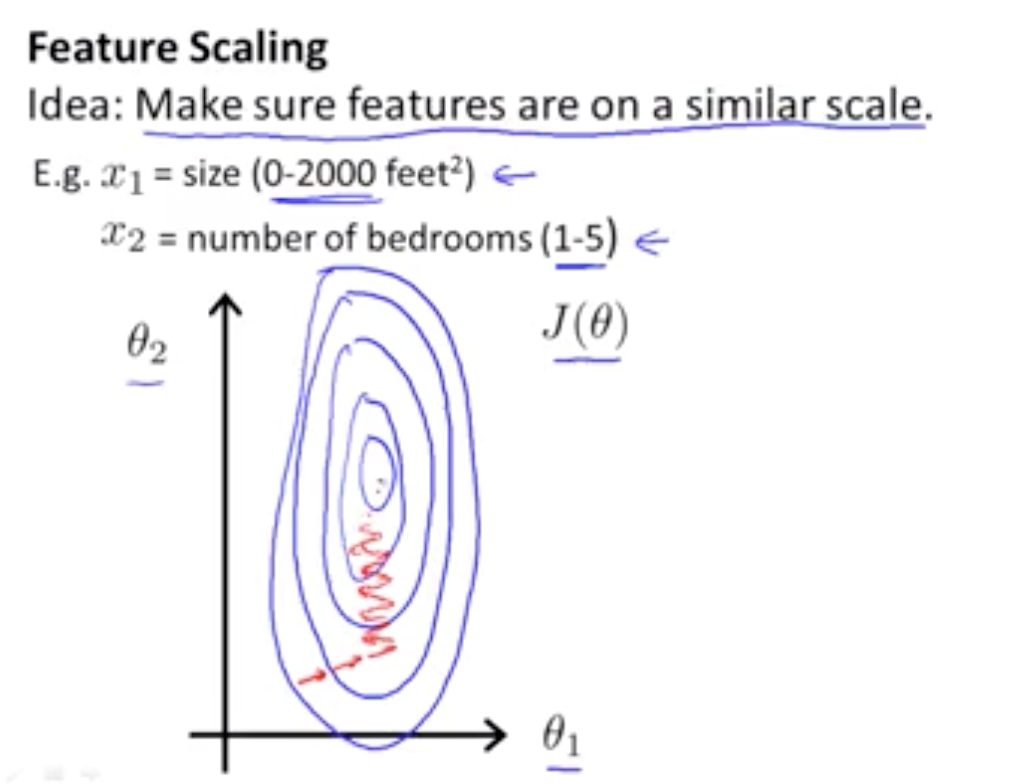
3.1 缩放目的
这个问题有多个特征 如果你能确保这些特征 都处在一个相近的范围 我的意思是确保 不同特征的取值 在相近的范围内
下面举一个反面例子:假如你有一个具有两个特征的问题 其中 x1 是房屋面积大小 它的取值 在0到2000之间 x2 是卧室的数量 可能这个值 取值范围在1到5之间 如果你画出代价函数 J(θ) 的轮廓图
3.2 缩放(特征缩放其实并不需要太过准确,只是为了加速梯度下降)
1. 不用过于担心 你的特征是否在完全 相同的范围或区间内
但是只要他们都 只要它们足够接近的话 梯度下降法就会正常地工作2. 均值规范化处理
其中,S为标准差(实际上,用最大值-最小值也是可以的),miu为均值4. 学习率alpha的选择
通过损失函数的图像判断
5. 特征 和 多项式回归(polynomial regression)【和多元相对应】
5.1 选择特征的方法
有时 通过定义 新的特征 你确实会得到一个更好的模型 与选择特征的想法
We can combine multiple features into one. For example, we can combine x1 and x2 into a new feature x3 by taking x1⋅x2.
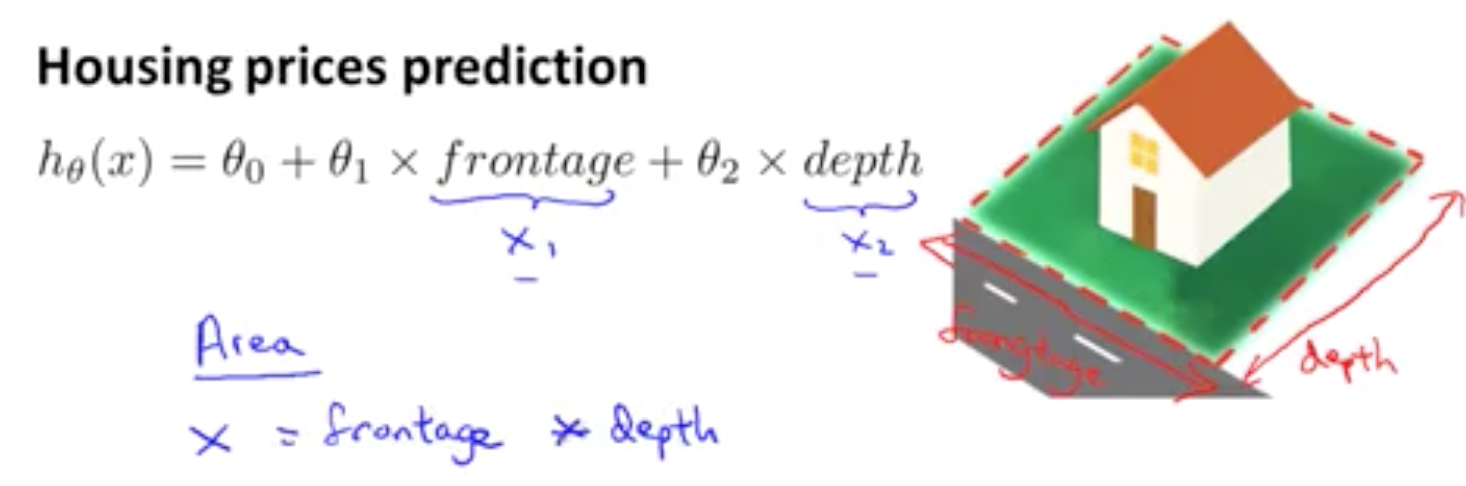
以预测房价为例 假设你有两个特征 分别是房子临街的宽度和垂直宽度 这就是我们想要卖出的房子的图片 临街宽度 被定义为这个距离 其实就是它的宽度 或者说是 你拥有的土地的宽度 如果这块地都是你的的话 而这所房子的 纵向深度就是 你的房子的深度 这是正面的宽度 这是深度 我们称之为临街宽度和纵深 你可能会 像这样 建立一个 线性回归模型 其中临街宽度 是你的第一个特征x1 纵深是你的第二个 特征x2 但当我们在 运用线性回归时 你不一定非要直接用 给出的 x1 和 x2 作为特征 其实你可以自己创造新的特征 因此 如果我要预测 房子的价格 我真正要需做的 也许是 确定真正能够决定 我房子大小 或者说我土地大小 的因素是什么 因此 我可能会创造一个新的特征 我称之为 x 它是临街宽度与纵深的乘积 5.2 如何得到不同的学习算法
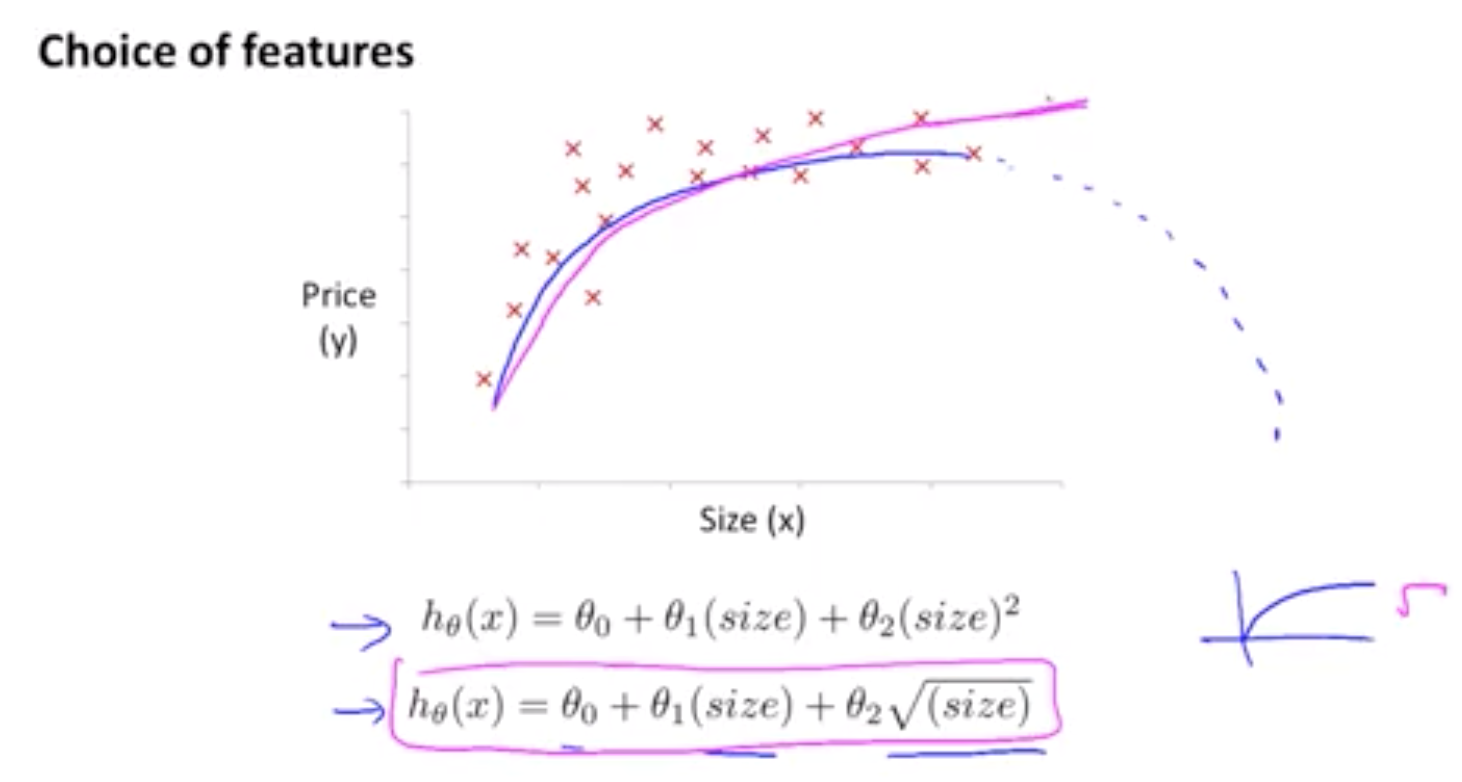
如何将一个 多项式 如一个二次函数 或一个三次函数拟合到你的数据
Our hypothesis function need not be linear (a straight line) if that does not fit the data well.
We can change the behavior or curve of our hypothesis function by making it a quadratic, cubic or square root function (or any other form).6. 正规方程
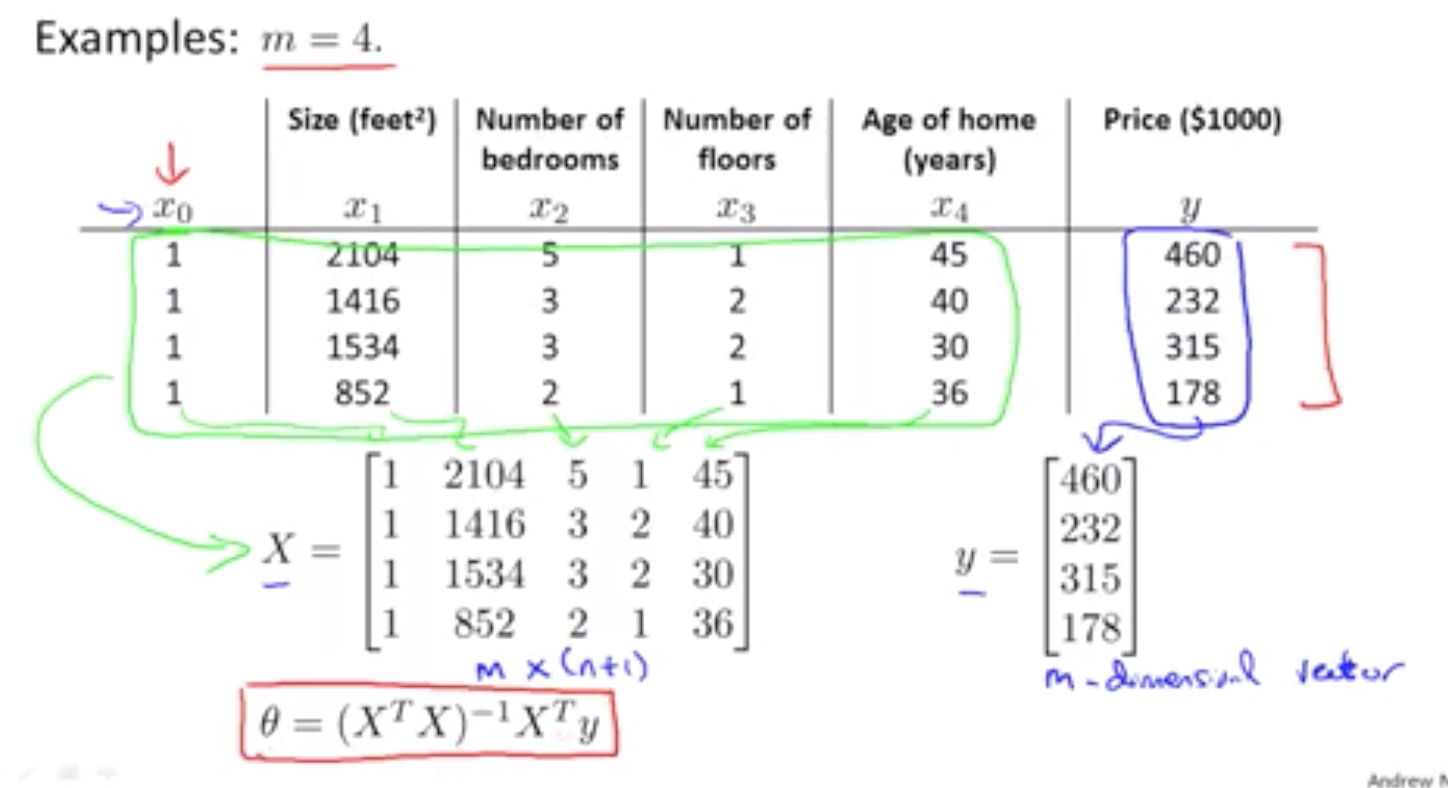
对于某些线性回归问题 它给出了一个更好的方法 求出参数 θ 的最优解
相对于梯度下降一步步求到最优解,正规方程法,提供了一种求theta的解析接发,可以一次性求解theta的最优解
6.1 正规方程直观理解
6.2 如何选择梯度下降 和 正规方程法(只适用于线性回归)
只要特征变量的数目并不大 正规方程是一个很好的 计算参数 θ 的替代方法 具体地说 只要特征变量数量小于一万 具体地说 只要特征变量数量小于一万 我通常使用正规方程法 我通常使用正规方程法 而不使用梯度下降法
6.3 正规方程的不可逆性
当你发现的矩阵X'X的结果是奇异矩阵 或者找到的其它矩阵是不可逆的 我会建议你这么做 首先 看特征值里是否有一些多余的特征