Welcome to MyBlog!
本文所以截图以及文字均来自于:Coursera
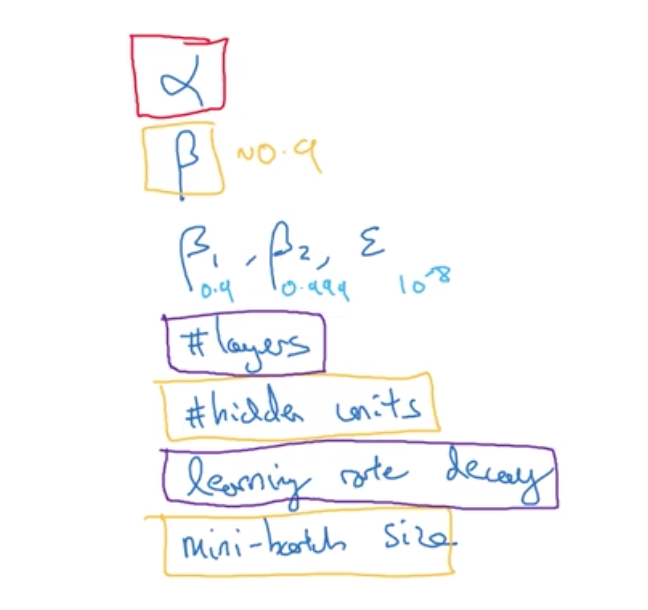
1. 重要性排序
红色>黄色>紫色
2. 怎么样选择超参数的抽样?
2.1. 随机抽样 try random values:Don’t use a grid(网格)
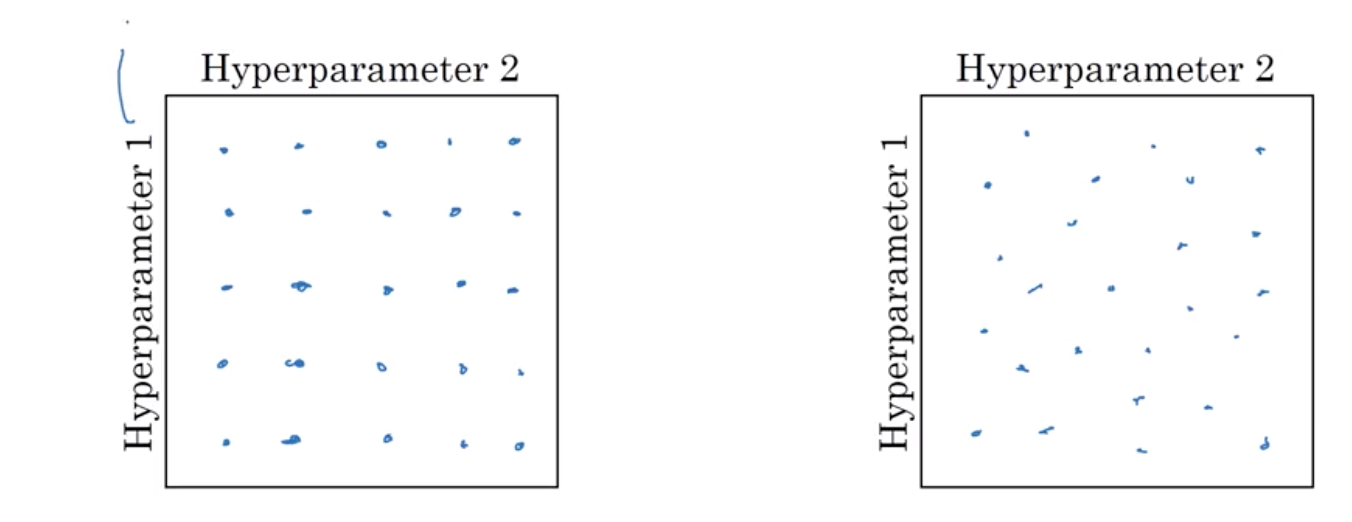
如果你有两个超参数 假设是超参数1和超参数2 人们经常会像这样 在一个网格中对点进行取样 然后系统化地尝试这些点所代表的值 在这里我放的是一个5*5的网格 实际上可能比这个大 或者比这个小 在这个例子中 当你尝试过所有25个点后 选择最优的超参数 当超参数的数量相对较少时 这样的取参方法较为实用 但是在深度学习中 我推荐你采取另一种方法 在网格中进行随机取样 像这样随机选择一些点 同样的 我们选择25个点 然后在这些随机选取的点中 尝试所有的超参数 这样做的原因是 事先你很难知道 在你的问题中 哪个超参数是最重要的
很明显,从下图可以看出,在hyperparameter1重要性远大于hyperparameter2的前提下,右➡️图的有效结果远大于⬅️图,这样找到理想的参数组合的概率就变大了。
2.2. 区域定位的抽样方案(coarse粗 to fine精)
比如在这个二维的例子中 你抽取了这些点 也许你发现这个点能产生最好的结果 并且旁边的一些点的结果也不错 那么在这个方案中 你需要做的是对 这些点所在的区域进行限定 然后在这个区域内进行密度更高的抽样 或者依然选择随机抽样 但是需要把更多资源集中在这个蓝色方块中搜索 前提是你大体能确定这个区域内取的值能产生最优结果 即最理想的超参数来自于这个区域 在对整个框定范围进行粗略的抽样后 结果会引导你集中在一个更小的区域内 然后你可以在更小的方块内 进行更密集的抽样
2.3. 选择合适的尺度来随机抽样
比如你正在搜索超参数alpha,即学习率 假设你认为它的下限是0.0001 上限是1 现在画出从0.0001
1的数轴 并均匀随机地抽取样本值 那么90%的样本值将落在0.11的范围内 即你用90%的资源搜索0.11 只有10%的资源用于搜索0.00010.1范围内的值 看起来不大对 更合理的方法似乎应该以对数尺度(log scale)来搜索 而不是用线性尺度(linear scale)
2.4. 特例:beta
,用0.9计算指数加权平均值 相当于计算最后10个值的平均值 比如计算10天气温的平均值 而使用0.999就相当于计算1000个值的平均值 类似上一页ppt所展示,如果你要搜索 0.9
0.999的范围,线性尺度的取样 即均匀的,随机的,0.9至0.999范围内的搜索,没什么意义 那么考虑这个问题的最好的方法是 将这个范围展开为1-beta 得到0.10.001的范围 那么我们对beta的采样范围 为0.10.001 现在运用我们之前学到的方法 这是10^(-1),这是10^(-3) 请注意,之前的数轴是从左至右递增的 这里我们要反过来 大的值在左边,小的值在右边 所以你要做的是在-3-1的范围内均匀随机的取样 然后置1-beta=10^r,即beta=1-10^r 就得到了这个超参数在适当尺度上 的随机取样值 希望这能解释: 你在探索0.90.99和0.990.999的范围时 使用了同样数量的资源 如果你想要知道关于这个做法的更规范的数学证明 也就是说,为什么以线性尺度取样是个坏主意? 这是因为随着beta趋近于1
其结果对于beta的改变非常敏感 即使是对beta非常小的改变 如果beta从0.9变成0.9005 这没什么大不了,你的结果几乎没有任何变化 但是如果beta从0.999变成0.9995 它将会对你正在运行的算法产生巨大的影响 在前一个例子中,都是取大约10个值的平均 但是这里,取指数加权平均的情况下 它从取最后1000个样例变成了取最后2000个样例的平均 因为我们的公式是1/(1-beta) 所以当beta趋近于1时,它对beta的改变非常敏感 那么上述整个取样过程所做的 就是使你在beta趋近于1的区域内以更大的密度取样
2.5. 如何如何有规划地 探寻合适超参数的小技巧
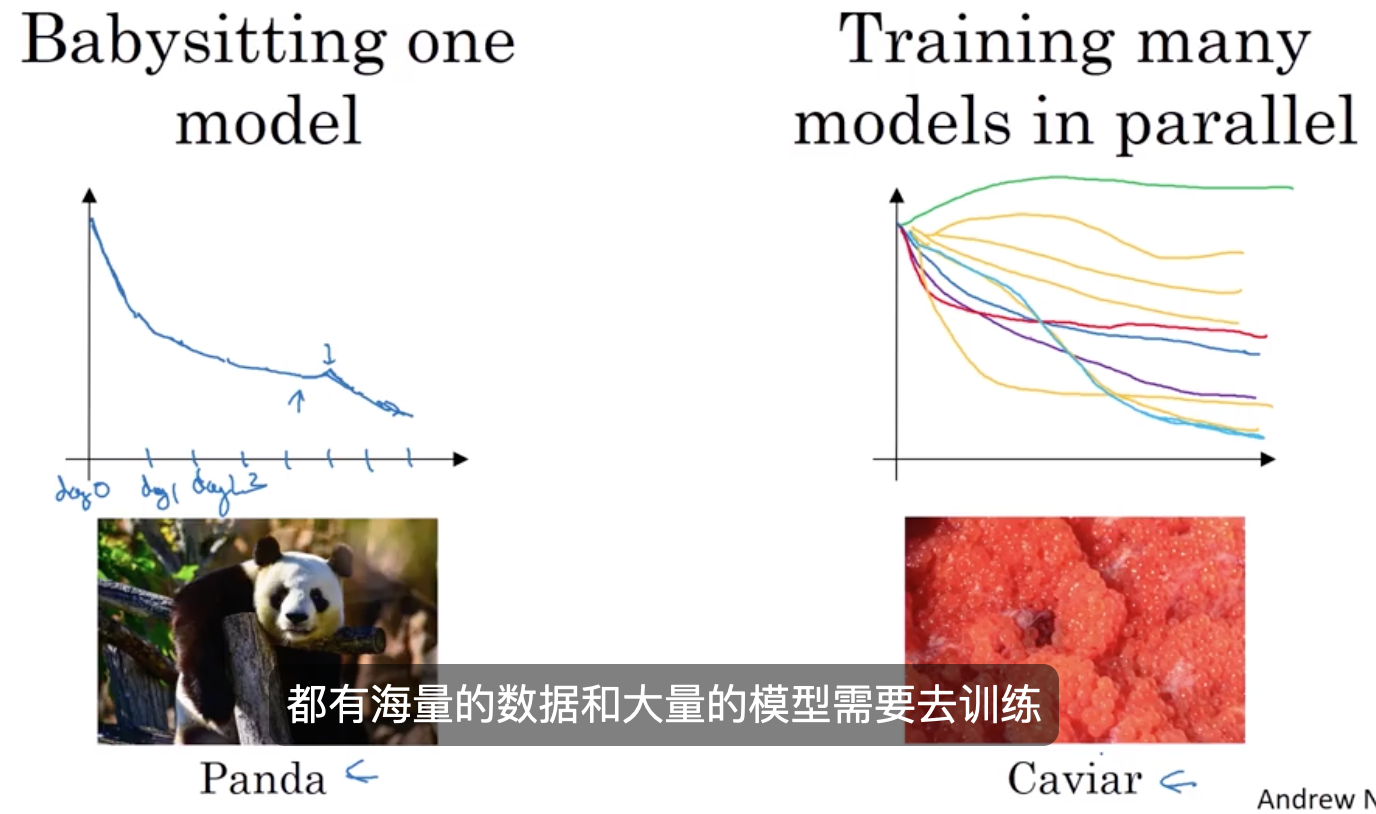
pandas vs caviar(鱼子酱)
两种模式的选择主要取决于你的运算资源
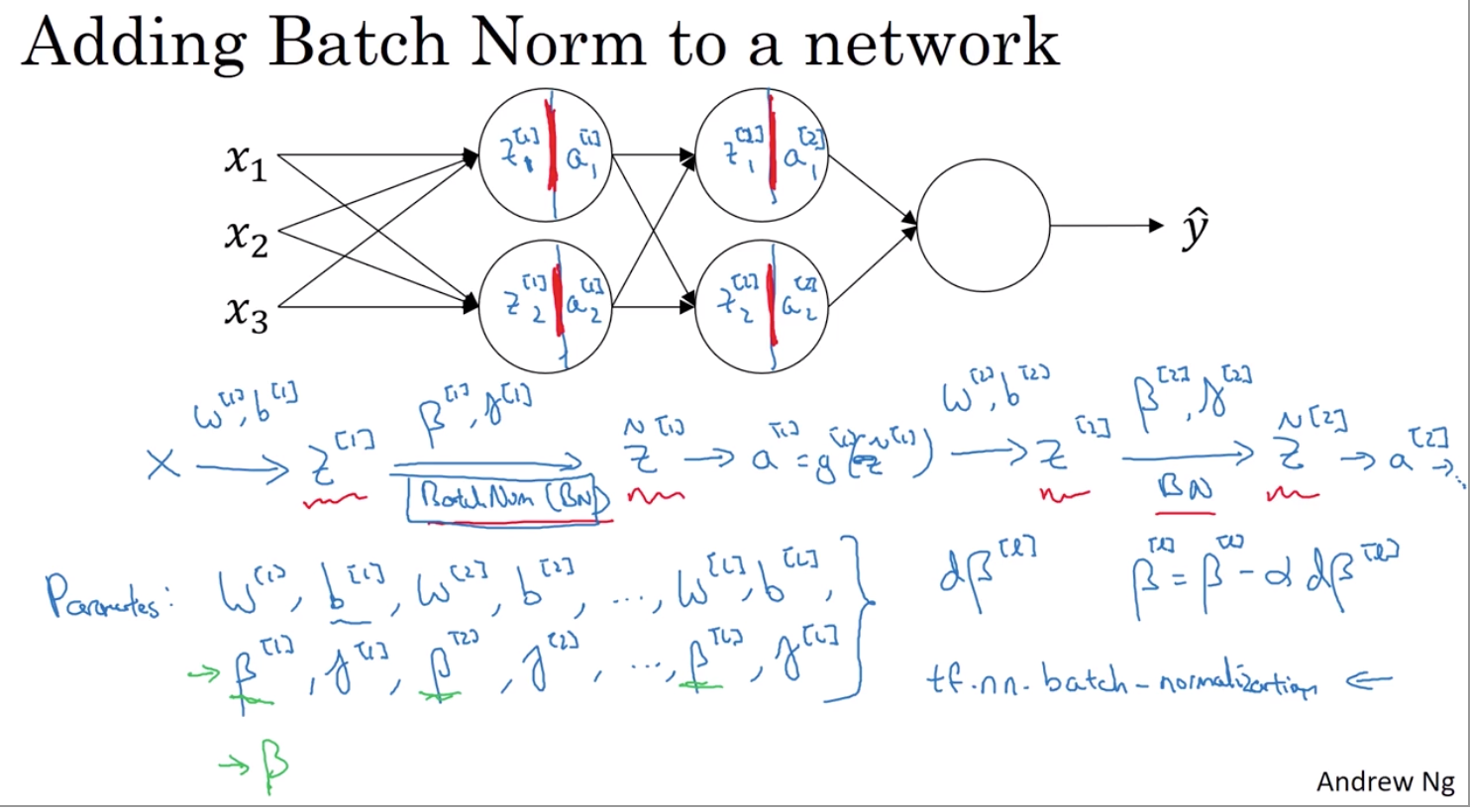
3. 批量标准化(batch norm) (针对W)
可以让你的超参搜索变得很简单 让你的神经网络变得更加具有鲁棒性 可以让你的神经网络对于超参数的选择上不再那么敏感 而且可以让你更容易地训练非常深的网络
上图中的标准化公式的分母有错误
每一组z都是均值0方差1 但是我们并不希望所有的隐藏单元都是这样的 也许本身它们的分布就有不同 所以我们可以这么做 z tilde = γ * zi * norm + β 这里的γ和β值可以从你的模型中学习
3.1. BN算法在神经网络的工作原理
BN算法和普通的输入层标准化的不同在于引入了gama和beta
3.2 BN算法有效的原因
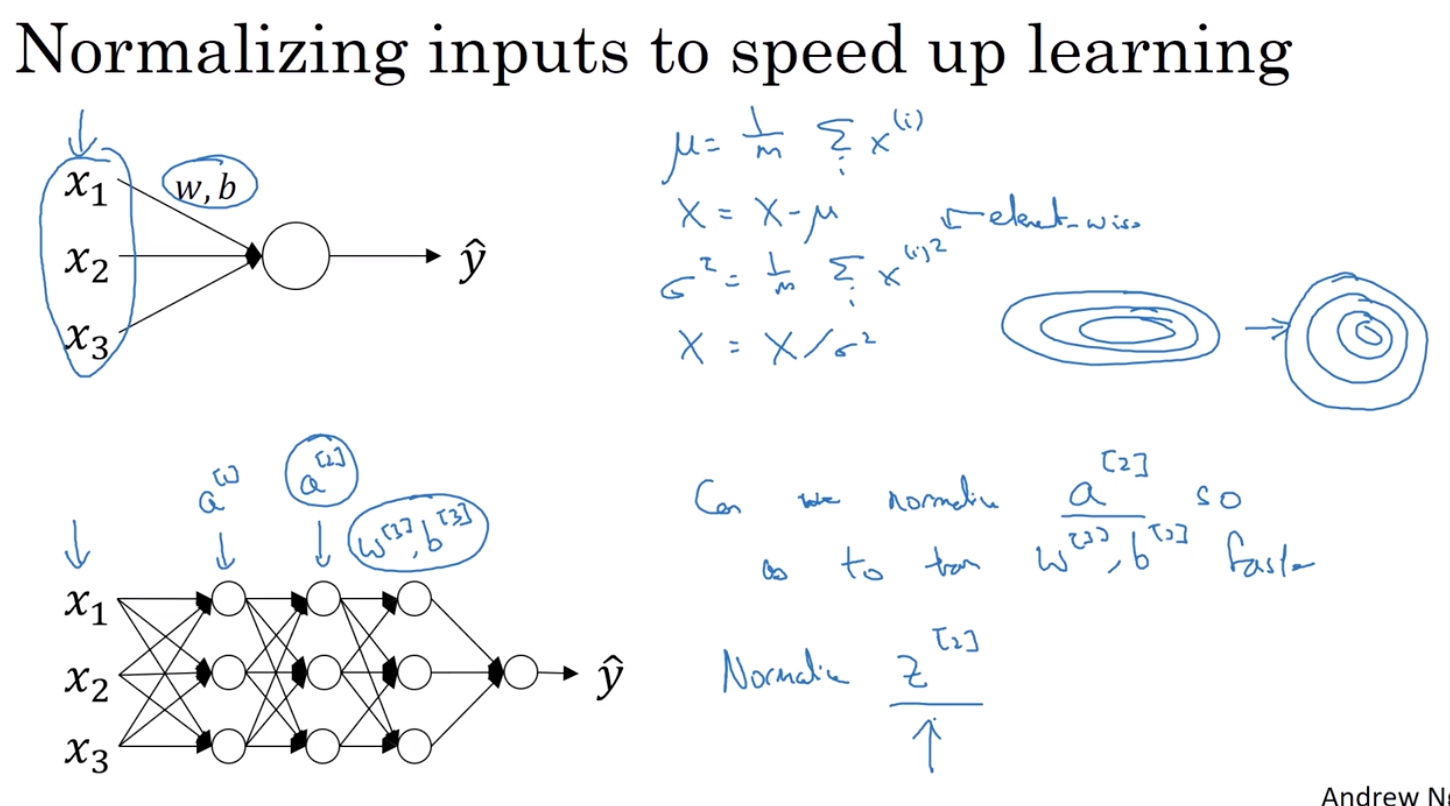
- 我们看到经过归一化的输入特征(用X表示) 它们的均值为0 方差为1 这将大幅加速学习过程 所以与其含有某些在0到1范围内变动的特征 或在1到1000范围内变动的特征 通过归一化所有输入特征X 让它们都拥有相同的变化范围将加速学习 所以 BN算法有效的一个原因是 它同样如此 只不过它应用于隐藏层的值 而不是这里输入特征
- 它产生权重 (w参数) 在深层次网络中,解决了协变量问题
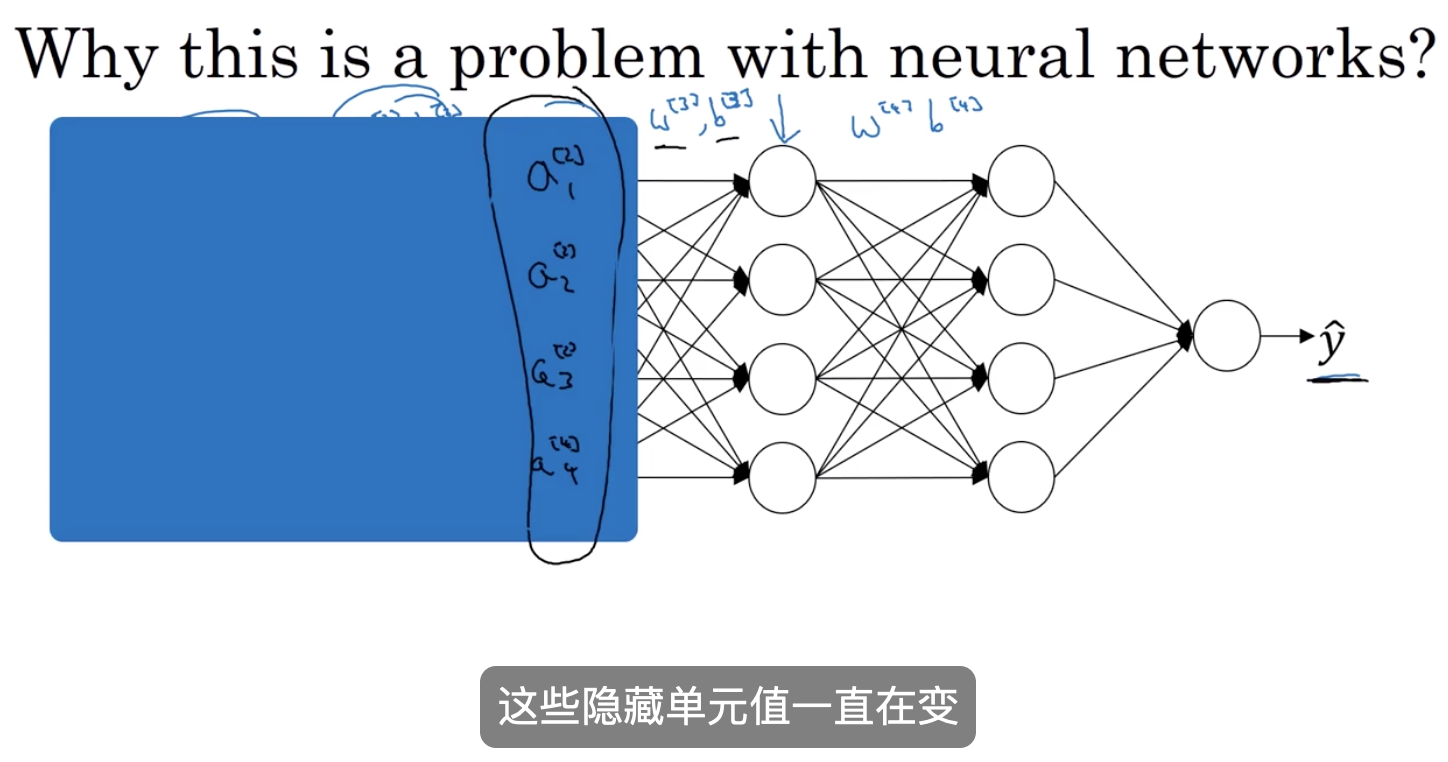
所以从第三级隐藏层角度来看 这些隐藏单元值一直在变 所以它受协变量问题影响 所以它受协变量问题影响 这在之前我们谈过 所以BN算法所做的就是 它减少了这些隐藏单元值的 分布的不稳定性
BN算法确保的是无论它怎么变 z21和z22的均值和方差将保持不变 所以尽管z21和z22的值变化 它们的均值一直为0 方差一直为1 或者 并不一定是均值0 方差1 但是它们的值由beta2 gamma2控制 这两个参数由神经网络选定 所以可以使均值为0 方差为1 或者 可以是其它任何均值和方差 但是这样做 限制了先前层中参数的更新 对第三层 现在所看到和要学习的值的分布的 影响 对第三层 现在所看到和要学习的值的分布的 影响 所以 BN算法减少输入值变化所产生的问题 它的确使这些值变得稳定 所以神经网络的后层 可以有更加稳固的基础 尽管输入分布变化了一点 它变化的更少 实际是 尽管前几层继续学习 后面层适应前面层变化的力量被减弱 后面层适应前面层变化的力量被减弱 如果我们愿意 BN算法削弱了 前面层参数和后层参数之间的耦合 前面层参数和后层参数之间的耦合 所以它允许网络的每一层独立学习 有一点独立于其它层的意思 所以这将有效提升整个网络学习速度
- 它具有轻微的正则化效果
因为我们在该min-batch上计算了均值和方差,而不是在整个数据集上计算,所以该均值和方差包含有噪声,因为它是由相对较少的数据集评估得来**(batch越大噪音越小)**,该归一化过程 从zl 到 (带波浪号的)zl, 这个过程也会产生噪声, 因为它是用带有一定噪声的均值和方差来计算的 所以和dropout算法类似, 它会为每个隐藏层的激活函数增加一些噪声, dropout有噪声的原因是 它将隐藏单元以一定概率乘以0, 以一定概率乘以1
3.3 在测试数据上使用BN
训练过程中,(流程: 训练 train ,开发 Dev,测试 test )我们是在每个 mini-batch 使用 Batch Norm,来计算所需要的均值μ和方差σ2。但是在测试的时候,我们需要对每一个测试样本进行预测,无法计算均值和方差。
此时,我们需要单独进行估算均值 μ和方差σ2。通常的方法就是在我们训练的过程中,对于训练集的 mini-batch ,使用指数加权平均,当训练结束的时候,得到指数加权平均后的均值 μ 和方差σ2
,而这些值直接用于 Batch Norm 公式的计算,用以对测试样本进行预测