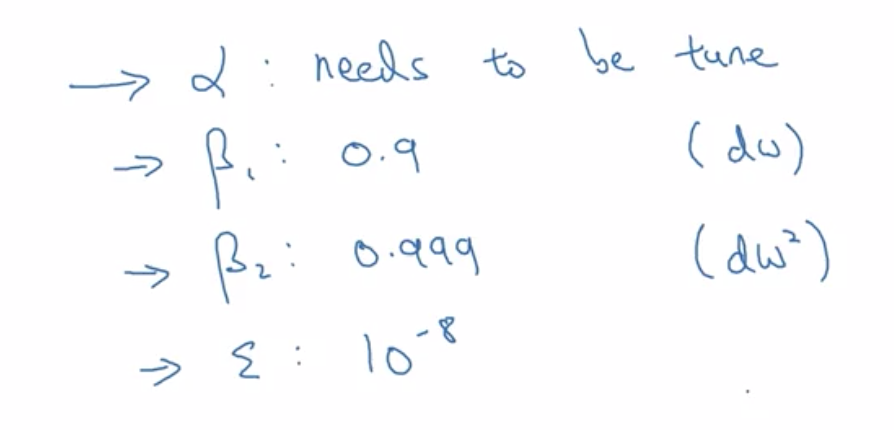Welcome to MyBlog!
本文所以截图以及文字均来自于:Coursera
1 小批量梯度下降算法(mini-batch gradient descent)
首先将你的训练集拆分成更小的 微小的训练集 即小批量训练集(mini-batch) 比如说每一个微型训练集只有1000个训练样例 也就是说 取x1至x1000作为第一个微训练集 也叫做小批量训练集 然后取接下来的1000个样例 x1001至x2000这1000个样例 依次继续
将mini-batch极端的设置为m,就得到了批量梯度下降
极端地设置为1,就得到了随机梯度下降
两种方法的区别:批量梯度下降算法可能从这里开始 它的噪声相对小些 每一步相对大些 并且最终可以达到最小值 而相对的 随机梯度下降算法 让我们选一个不同的点 假使从这里开始 这时对于每一次迭代你就在一个样本上做梯度下降 大多数时候你可以达到全局最小值 但是有时候也可能因为某组数据不太好 把你指向一个错误的方向 因此随机梯度算法的噪声会非常大 一般来说它会沿着正确的方向 但是有事也会指向错误的方向 而且随机梯度下降算法 最后也不会收敛到一个点 它一般会在最低点附近摆动 但是不会达到并且停在那里 实际上 mini-batch的大小一般会在这2个极端之间
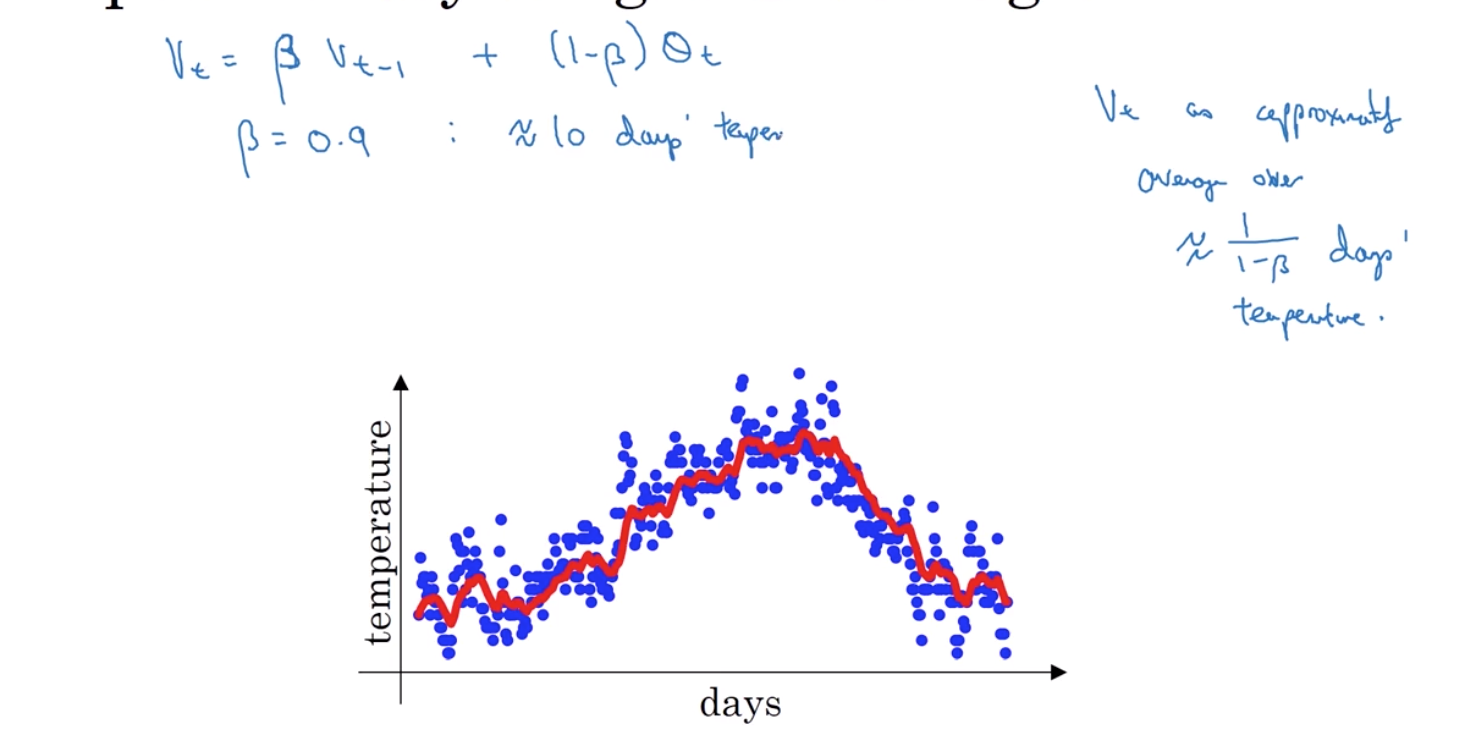
2 指数加权(滑动)平均
beta*V_(t-1)加上 之前使用的是0.1 现在把它换成(1-beta)*theta_t 之前beta=0.9 出于我们之后会讲的某些原因 当你计算这个公式的时候 你可以认为V_t近似于 1/(1-beta)天温度的平均 举例来说 当beta=0.9的时候 你可以认为它是前10天的气温平均值
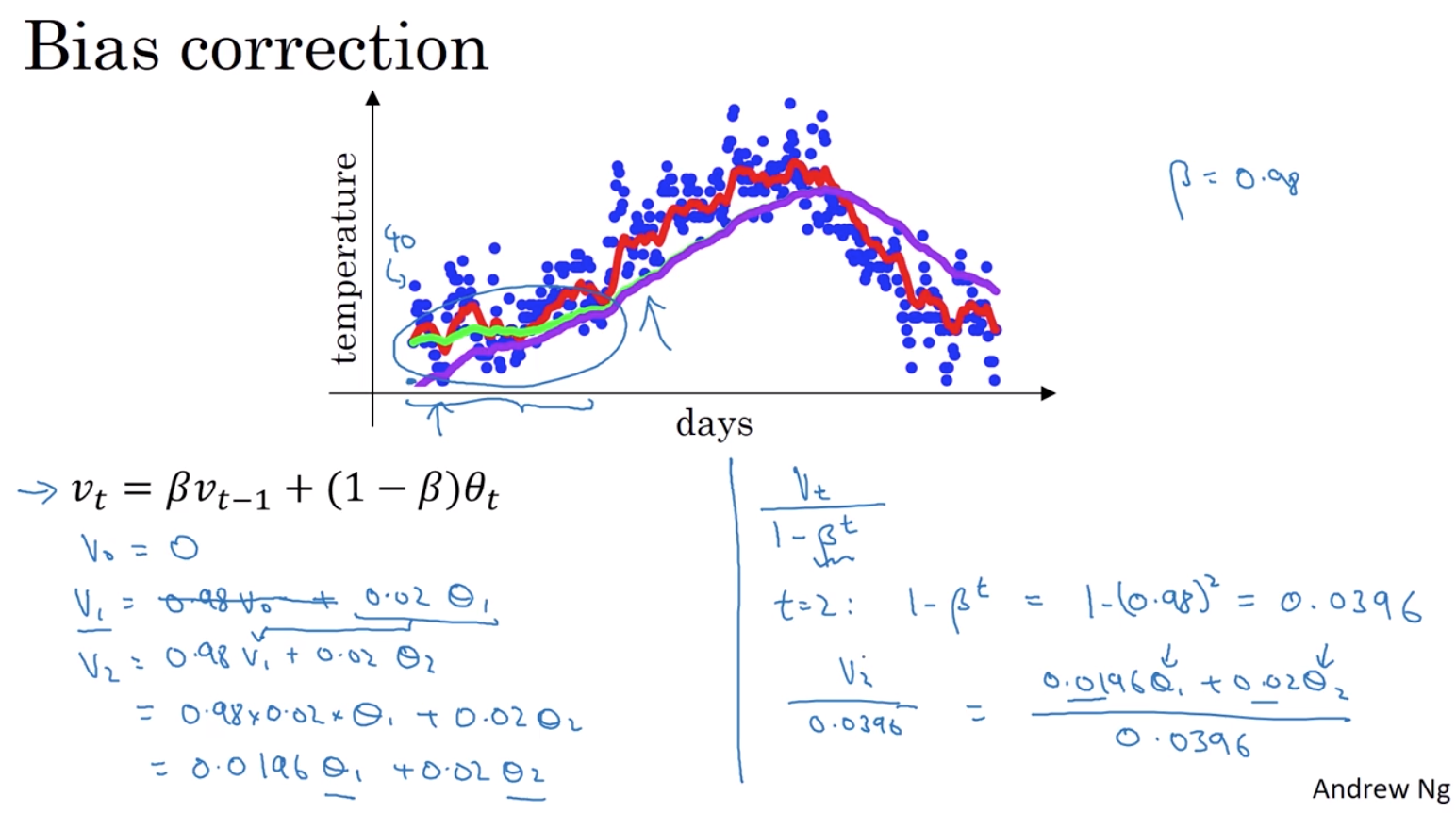
3 偏差修正
它能够帮助你更好地计算平均值
工作原理:用vt/1-βt代替vt(t是下标)
在机器学习中 多数的指数加权平均运算 并不会使用偏差修正 因为大多数人更愿意在初始阶段 用一个稍带偏差的值进行运算 不过 如果在初始阶段就开始考虑偏差 指数加权移动均指仍处于预热阶段 偏差修正可以帮你尽早做出更好的估计
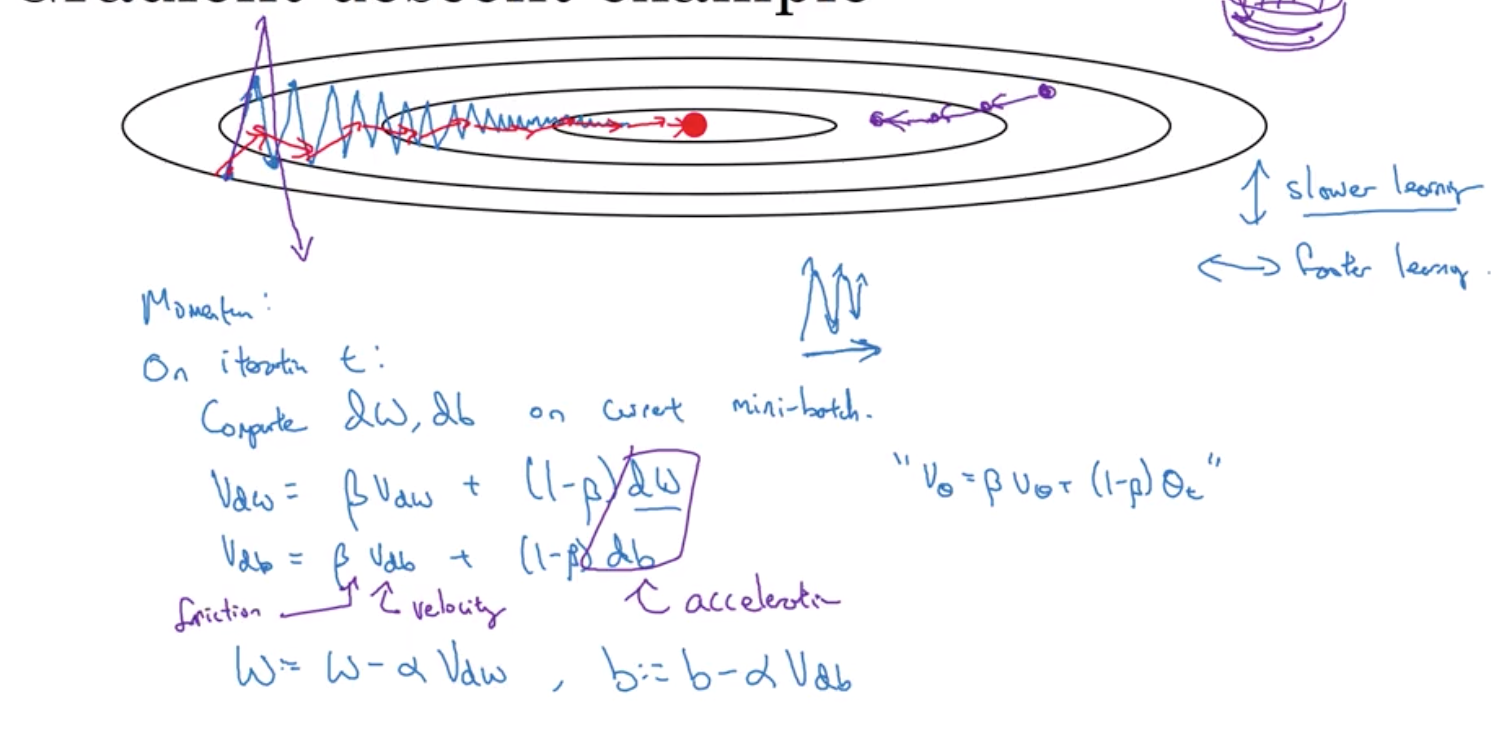
4 动量梯度下降算法
它几乎总会比标准的梯度下降算法更快 一言以蔽之 算法的主要思想是 计算梯度的指数加权平均 然后使用这个梯度来更新权重
可以减少震荡,原因:如果把这些梯度平均一下 你会发现这些震荡 在纵轴上的平均值趋近于0 所以 在垂直方向上 你会希望减慢速度 正数和负数在计算平均时相互抵消了 平均值接近于0 然而在水平方向上 所有导数都指向水平方向的右边 所以水平方向的平均值仍然较大 因此在数次迭代之后 你会发现动量梯度下降算法的每一步 在垂直方向上的振荡非常小 且在水平方向上运动得更快 这会让你的算法选择更加直接的路径 或者说减弱了前往最小值的路径上的振荡
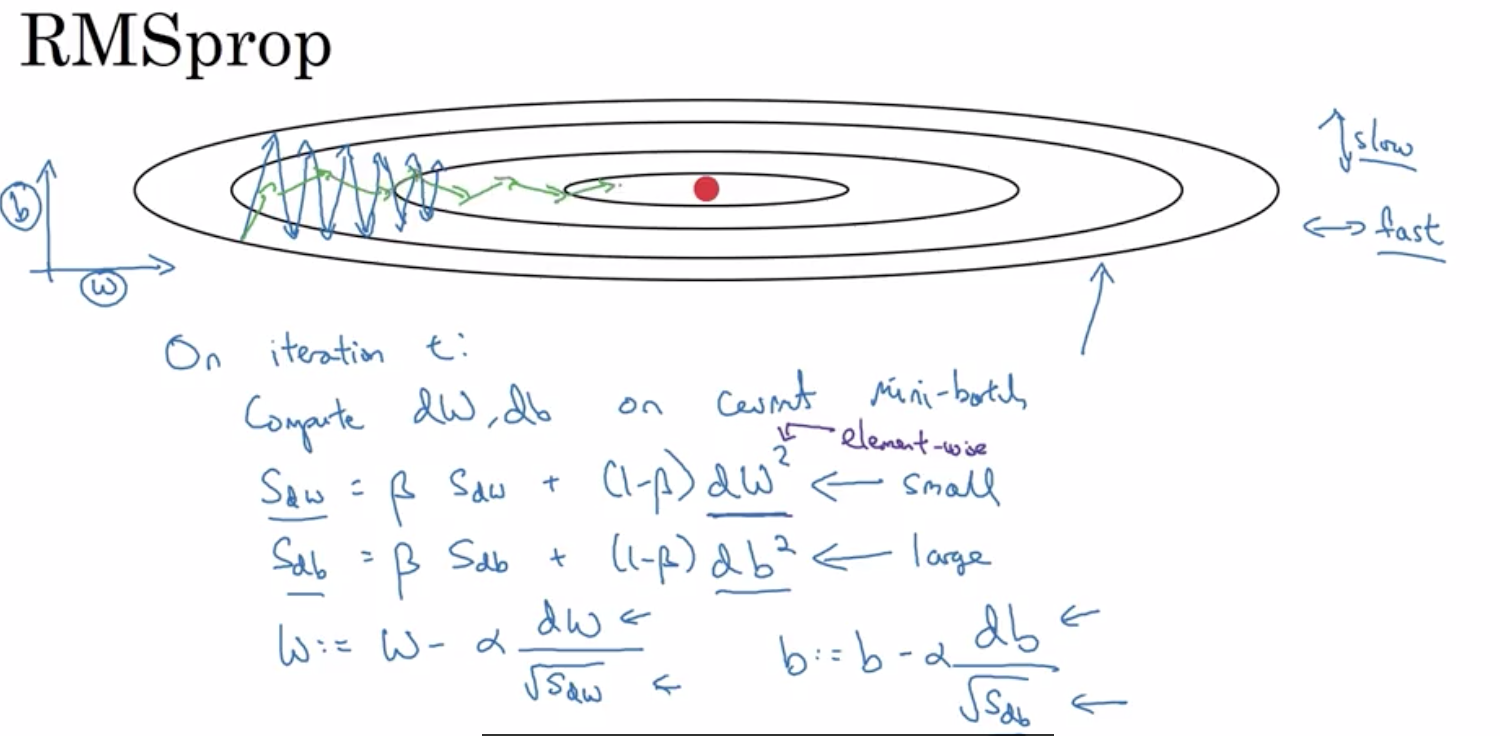
5 RMSprop 均方根传递(root mean square prop)
你希望减慢b方向的学习 也就是垂直方向 同时加速或至少不减慢水平方向的学习 这就是RMSprop算法要做的
现在我们来理解一下它的工作原理 记得在水平方向上 即例子中W的方向上 我们希望学习速率较快 而在垂直方向上 即例子中b的方向上 我们希望降低垂直方向上的振荡 对于S_dW和S_db这两项 我们希望S_dW相对较小 因此这里除以的是一个较小的数 而S_db相对较大 因此这里除以的是一个较大的数 这样就可以减缓垂直方向上的更新
另一个收效是 你可以使用更大的学习率alpha 学习得更快 而不用担心在垂直方向上发散
6 Adam优化算法(自适应矩估计Adaptive Moment Estimation)
Adam优化算法本质上是将 动量算法和RMSprop结合起来:在动量梯度下降算法抵消部分震荡的前提下,利用了rms梯度下降算法降低震荡
t表示迭代次数超参数的选择
7 学习率衰减 learning rate decay
如果你想使用学习率衰减 你可以尝试 不同的超参数组合 包括α0 以及这个衰减率的超参数 然后去尝试寻找一个效果好的数值
7.1 其他学习率衰减的方法
k表示常数
8 局部最优点,鞍点
对于一个高维空间的函数 如果梯度为零 则在每个方向上 它可能是凸函数 或者是凹函数 假设在一个 2万维的空间中 如果一个点要成为局部最优 则需要在所有的2万个方向上都像这样 因此这件事发生的概率非常低 大概2的负2万次方 你更有可能遇到的情况是
某些方向的曲线像这样向上弯曲 同时另一些方向的曲线则向下弯曲 并非所有曲线都向上弯曲 这就是为什么在高维空间中 你更有可能碰到一个像右图这样的鞍点 而不是局部最优
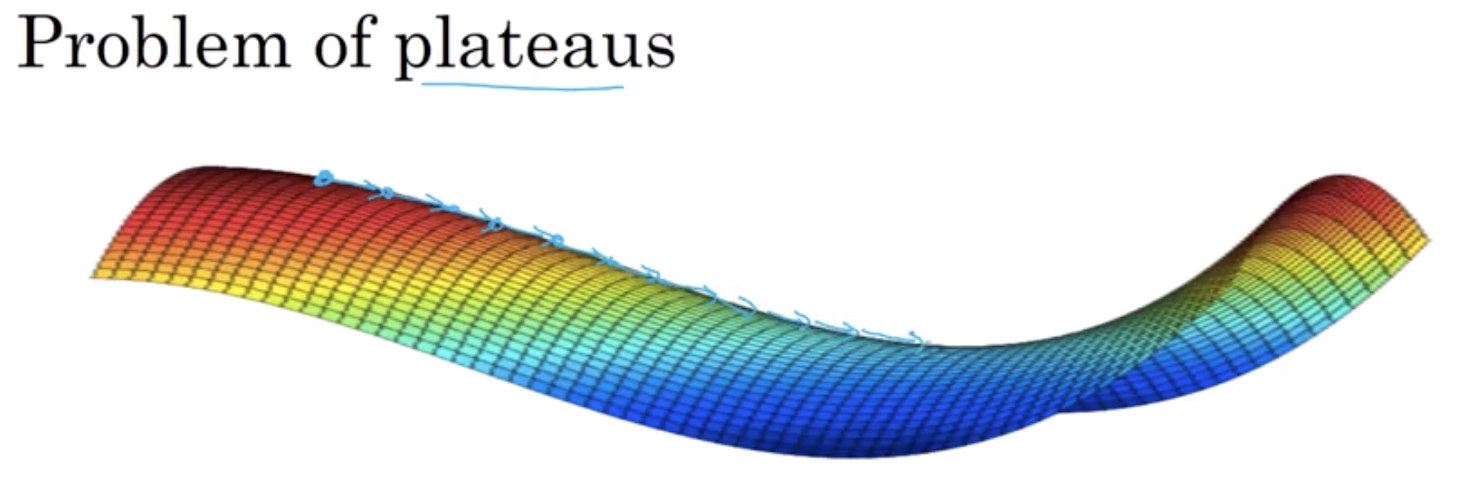
8.1 停滞区
实际上是停滞区(Plateaus) 停滞区指的是 导数长时间接近于零的一段区域 如果你在这里 那么梯度下降会沿着这个曲面向下移动 然而因为梯度为零或接近于零 曲面很平 你会花费很长的时间 缓慢地在停滞区里找到这个点 然后因为左侧或右侧的随机扰动,你的算法终于能够离开这个停滞区 它一直沿着这个很长的坡往下走, 直到抵达此处, 离开这个停滞区
首先 实际上你不太可能陷入糟糕的局部最优点 只要你训练的是一个较大的神经网络 有很多参数 代价函数J定义在一个相对高维的空间上
其次 停滞区是个问题, 它会让学习过程变得相当慢 这也是像动量(Momentum)算法
或RmsProp算法 或Adam算法能改善你的学习算法的地方